《2025年一遍过九年级初中数学上册人教版》

1 下列图形中表示的角是圆心角的是 ( )

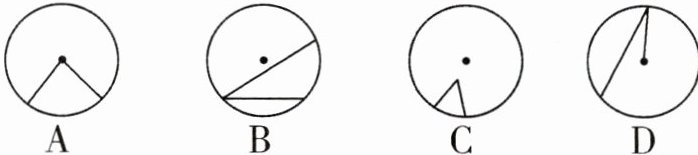
答案： A

2 在$\odot O$中,弦AB等于圆的半径,则它所对应的圆心角的度数为 ( )

A.$120^{\circ}$
B.$75^{\circ}$
C.$60^{\circ}$
D.$30^{\circ}$

答案：
C 如图,连接OA,OB.
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,即弦AB所对的圆心角的度数为60°.

3 教材P85T2变式[2025四平期末]如图,在$\odot O$中,AB是$\odot O$的直径,$\overset{\frown}{CB}= \overset{\frown}{CD}= \overset{\frown}{ED}$,$\angle AOE= 60^{\circ}$,则$\angle BOC$的度数为 ( )

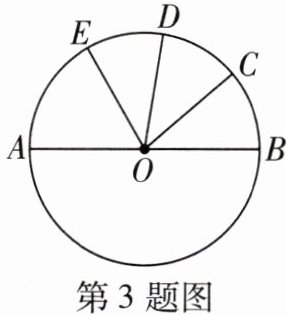
A.$40^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$

答案： A
∵AB是⊙O的直径,
∴∠AOE+∠BOE=180°,又
∵∠AOE=60°,
∴∠BOE=120°.
∵$\widehat{CB}=\widehat{CD}=\widehat{ED}$,
∴∠BOC=∠DOC=∠DOE=$\frac{1}{3}$∠BOE=40°.

4 [2025铁岭期中]如图,AB是$\odot O$的直径,点C,D在$\odot O$上,$AC= AD$,连接OC,OD,BC,$\angle AOD= 70^{\circ}$,则$\angle BCO$的度数是 ( )

A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$55^{\circ}$

答案： B
∵AC=AD,∠AOD=70°,
∴∠AOC=∠AOD=70°.
∵OB=OC,
∴∠B=∠BCO.又
∵∠AOC=∠B+∠BCO,
∴∠BCO=$\frac{1}{2}$∠AOC=35°.

5 [2024张家口桥西区期末]如图,点C是$\odot O$上的点,$CD\perp OA$于点D,$CE\perp OB$于点E,$CD= CE$,则$\overset{\frown}{AC}与\overset{\frown}{BC}$的关系是 ( )

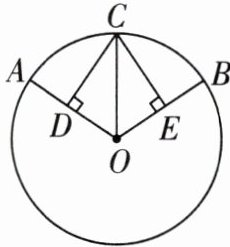
A.$\overset{\frown}{AC}= \overset{\frown}{BC}$
B.$\overset{\frown}{AC}＞\overset{\frown}{BC}$
C.$\overset{\frown}{AC}＜\overset{\frown}{BC}$
D.不能确定

答案： A
∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°.又
∵CD=CE,CO=CO,
∴Rt△COD≌Rt△COE(HL),
∴∠COD=∠COE,
∴$\widehat{AC}=\widehat{BC}$.

6 如图,点A,B,C都在$\odot O$上,点B是$\overset{\frown}{AC}$的中点,$\angle OBC= 50^{\circ}$,则$\angle AOB= $______$^{\circ}$.

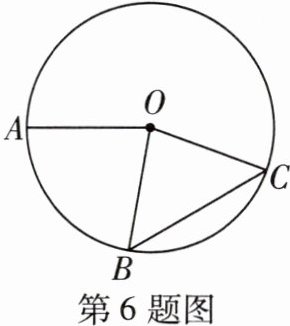
答案： 80
∵OB=OC,
∴∠OBC=∠OCB=50°,
∴∠BOC=180°-50°-50°=80°.
∵点B是$\widehat{AC}$的中点,
∴∠AOB=∠BOC=80°.

7 [2025南京联合体期中]如图,已知A,B,C,D是$\odot O$上的点,$\angle 1= \angle 2$,给出下列结论:①$\overset{\frown}{AB}= \overset{\frown}{CD}$;②$\overset{\frown}{BD}= \overset{\frown}{AC}$;③$AC= BD$;④$\angle BOD= \angle AOC$.其中结论正确的是______.(填序号)

答案： ①②③④
∵∠1=∠2,
∴$\widehat{AB}=\widehat{CD}$,∠1+∠BOC=∠2+∠BOC,即∠BOD=∠AOC,
∴AC=BD,$\widehat{BD}=\widehat{AC}$.故结论正确的是①②③④.

8 教材P89T4变式[2024衡阳南岳二中期末]如图,点A,B,C,D在$\odot O$上,且$AB= CD$.求证:$AC= BD$.

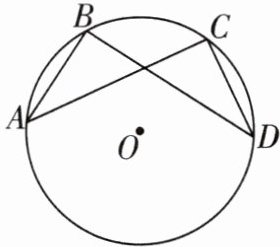
答案： 证明:
∵AB=CD,
∴$\widehat{AB}=\widehat{CD}$,
∴$\widehat{AB}+\widehat{BC}=\widehat{CD}+\widehat{BC}$,即$\widehat{AC}=\widehat{BD}$,
∴AC=BD.

9 一题多解[2025南阳内乡期末]如图,AB,CD是$\odot O$的弦,连接OA,OB.OC,OD分别交AB于点E,F,且$OE= OF$.求证:$\overset{\frown}{AC}= \overset{\frown}{BD}$.

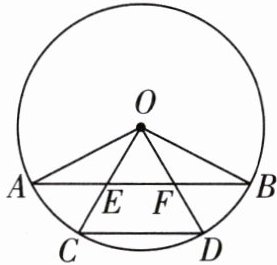
答案： 证明:证法一
∵OE=OF,
∴∠OEF=∠OFE.
∵OA=OB,
∴∠A=∠B.
∵∠OEF=∠A+∠AOC,∠OFE=∠B+∠BOD,(三角形外角的性质)
∴∠AOC=∠BOD,
∴$\widehat{AC}=\widehat{BD}$.
证法二 如图,过点O作OG⊥AB于点G,延长OG与⊙O交于点H.
∵OE=OF,OG⊥EF,
∴∠EOG=∠FOG(等腰三角形의三线合一),
∴$\widehat{CH}=\widehat{DH}$.同理可得$\widehat{AH}=\widehat{BH}$,
∴$\widehat{AH}-\widehat{CH}=\widehat{BH}-\widehat{DH}$,即$\widehat{AC}=\widehat{BD}$.
归纳总结 ⽤等腰三⾓形模型,通过作底边上的⾼利⽤三线合⼀的性质进⾏求解.