第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
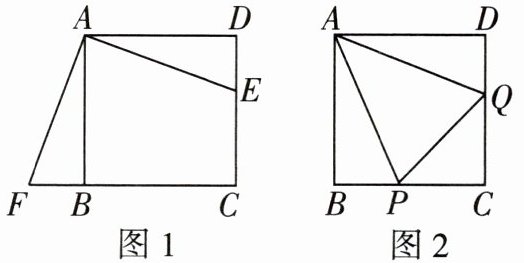
3 [2025德阳什邡中学期中](1)在正方形$ABCD$中,$E是CD$边上一点.将$\triangle ADE绕点A顺时针旋转90^{\circ}得到\triangle ABF$,如图1所示,观察可知,与$DE$相等的线段是____,与$\angle AFB$相等的角是____;
(2)如图2,在正方形$ABCD$中,$P$,$Q分别是BC$,$CD$边上的点,且$\angle PAQ = 45^{\circ}$,猜想线段$DQ$,$BP$,$PQ$间的数量关系,并证明;
(3)在图2中,连接$BD分别交AP$,$AQ于点M$,$N$,请写出$BM$,$DN$,$MN$间的数量关系,并说明理由.
(2)如图2,在正方形$ABCD$中,$P$,$Q分别是BC$,$CD$边上的点,且$\angle PAQ = 45^{\circ}$,猜想线段$DQ$,$BP$,$PQ$间的数量关系,并证明;
(3)在图2中,连接$BD分别交AP$,$AQ于点M$,$N$,请写出$BM$,$DN$,$MN$间的数量关系,并说明理由.

答案:
解:
(1)BF ∠AED
(2)DQ+BP=PQ.证明如下:
如图1,将△ADQ绕点A顺时针旋转90°得到△ABE,则∠D=∠ABE=90°.
∵∠ABP=90°,
∴∠ABE+∠ABP=180°,
∴点E,B,P共线.
由旋转的性质,知∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
在△APE和△APQ中,{AE=AQ,∠PAE=∠PAQ,AP=AP}
∴△APE≌△APQ(SAS),
∴PE=PQ,
∵PE=PB+BE=PB+DQ,
∴DQ+BP=PQ.
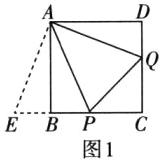
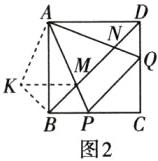
(3)BM²+DN²=MN².理由如下:
如图2,将△ADN绕点A按顺时针方向旋转90°得到△ABK,连接KM.
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质,得∠NAK=90°,∠ABK=∠ADN=45°,BK=DN,AK=AN.
∵∠PAQ=45°,
∴∠MAK=45°,
∴∠PAQ=∠MAK;
在△AMN和△AMK中,{AN=AK,∠NAM=∠KAM,AM=AM}
∴△AMN≌△AMK(SAS),
∴MN=MK.
∵∠MBA+∠KBA=90°,
∴△BMK为直角三角形,
∴BM²+BK²=MK²,
∴BM²+DN²=MN².
解:
(1)BF ∠AED
(2)DQ+BP=PQ.证明如下:
如图1,将△ADQ绕点A顺时针旋转90°得到△ABE,则∠D=∠ABE=90°.
∵∠ABP=90°,
∴∠ABE+∠ABP=180°,
∴点E,B,P共线.
由旋转的性质,知∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
在△APE和△APQ中,{AE=AQ,∠PAE=∠PAQ,AP=AP}
∴△APE≌△APQ(SAS),
∴PE=PQ,
∵PE=PB+BE=PB+DQ,
∴DQ+BP=PQ.


(3)BM²+DN²=MN².理由如下:
如图2,将△ADN绕点A按顺时针方向旋转90°得到△ABK,连接KM.
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质,得∠NAK=90°,∠ABK=∠ADN=45°,BK=DN,AK=AN.
∵∠PAQ=45°,
∴∠MAK=45°,
∴∠PAQ=∠MAK;
在△AMN和△AMK中,{AN=AK,∠NAM=∠KAM,AM=AM}
∴△AMN≌△AMK(SAS),
∴MN=MK.
∵∠MBA+∠KBA=90°,
∴△BMK为直角三角形,
∴BM²+BK²=MK²,
∴BM²+DN²=MN².
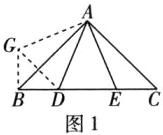
4 [2024梅州期中](1)如图1,在$\triangle ABC$中,$\angle CAB = 90^{\circ}$,$AB = AC$,$D$,$E为BC$上两点,且$\angle DAE = 45^{\circ}$.求证:$BD^{2} + CE^{2} = DE^{2}$.
(2)如图2,在$\triangle ABC$中,$\angle CAB = 120^{\circ}$,$AB = AC$,$\angle DAE = 60^{\circ}$,若以$BD$,$DE$,$EC为边的三角形是以BD$为斜边的直角三角形,当$BD = 2$时,求$DE$的长.
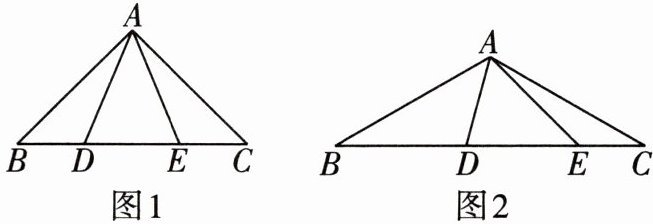
(2)如图2,在$\triangle ABC$中,$\angle CAB = 120^{\circ}$,$AB = AC$,$\angle DAE = 60^{\circ}$,若以$BD$,$DE$,$EC为边的三角形是以BD$为斜边的直角三角形,当$BD = 2$时,求$DE$的长.

答案:
解题思路:要证明BD²+CE²=DE²,该等式看起来是勾股定理的形式,故需将BD,CE,DE三条线段放置到同一个三角形中,再证明这个三角形是直角三角形即可,而旋转是全等变换,故可以通过旋转将零散的线段变换到规则图形中
(1)证明:如图1,把△ACE绕点A顺时针旋转90°,得到△ABG,连接DG,
则△ACE≌△ABG,
∴AG=AE,BG=CE,∠ABG=∠ACE.
∵∠GAE=90°,∠DAE=45°,
∴∠GAD=∠DAE=45°.
在△ADG和△ADE中,{AG=AE,∠GAD=∠EAD,AD=AD}
∴△ADG≌△ADE(SAS),
∴ED=GD.
∵∠BAC=90°,
∴∠ACE+∠ABC=90°,
∴∠ABG+∠ABC=90°,
∴∠GBD=90°,
∴BD²+BG²=DG²,即BD²+CE²=DE².

(2)解:如图2,将△AEC绕点A顺时针旋转120°,得到△AFB,连接DF,
则△AEC≌△AFB,
∴AF=AE,∠ABF=∠ACB,EC=BF,∠EAF=120°.
∵∠CAB=120°,AB=AC,
∴∠ABC=∠ACB=∠ABF=30°,
∴∠FBD=60°.
∵∠EAF=120°,∠EAD=60°,
∴∠DAE=∠DAF=60°,
又AE=AF,AD=AD,
∴△ADE≌△ADF(SAS),
∴DF=DE.
∵以BD,DE,EC为边的三角形是以BD为斜边的直角三角形,
∴以BD,DF,BF为边的三角形是直角三角形,且BD是斜边,
∴△BDF是直角三角形,∠BFD=90°,
∵∠FBD=60°,
∴∠FDB=30°,
∴BD=2BF=2EC=2,
∴BF=EC=1,
∴DE=DF=√(BD² - BF²)=√3;
解题思路:要证明BD²+CE²=DE²,该等式看起来是勾股定理的形式,故需将BD,CE,DE三条线段放置到同一个三角形中,再证明这个三角形是直角三角形即可,而旋转是全等变换,故可以通过旋转将零散的线段变换到规则图形中
(1)证明:如图1,把△ACE绕点A顺时针旋转90°,得到△ABG,连接DG,
则△ACE≌△ABG,
∴AG=AE,BG=CE,∠ABG=∠ACE.
∵∠GAE=90°,∠DAE=45°,
∴∠GAD=∠DAE=45°.
在△ADG和△ADE中,{AG=AE,∠GAD=∠EAD,AD=AD}
∴△ADG≌△ADE(SAS),
∴ED=GD.
∵∠BAC=90°,
∴∠ACE+∠ABC=90°,
∴∠ABG+∠ABC=90°,
∴∠GBD=90°,
∴BD²+BG²=DG²,即BD²+CE²=DE².


(2)解:如图2,将△AEC绕点A顺时针旋转120°,得到△AFB,连接DF,
则△AEC≌△AFB,
∴AF=AE,∠ABF=∠ACB,EC=BF,∠EAF=120°.
∵∠CAB=120°,AB=AC,
∴∠ABC=∠ACB=∠ABF=30°,
∴∠FBD=60°.
∵∠EAF=120°,∠EAD=60°,
∴∠DAE=∠DAF=60°,
又AE=AF,AD=AD,
∴△ADE≌△ADF(SAS),
∴DF=DE.
∵以BD,DE,EC为边的三角形是以BD为斜边的直角三角形,
∴以BD,DF,BF为边的三角形是直角三角形,且BD是斜边,
∴△BDF是直角三角形,∠BFD=90°,
∵∠FBD=60°,
∴∠FDB=30°,
∴BD=2BF=2EC=2,
∴BF=EC=1,
∴DE=DF=√(BD² - BF²)=√3;
查看更多完整答案,请扫码查看


