《2025年一遍过九年级初中数学上册人教版》

8 如图,两个五角星关于某一点中心对称,则对称中心和点A的对称点是( )

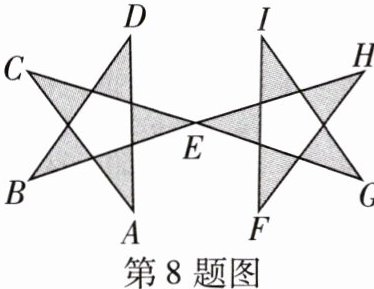
A.A和H
B.I和E
C.E和F
D.E和I

答案：
D 如图，连接对称点可知，点E是对称中心，点A的对称点是点I.

9 [2025吴忠三中期中]如图,$\triangle ABC和\triangle DEC$关于点C中心对称,若$AC= 1$,$AB= 2$,$∠BAC= 90^{\circ}$,则AE的长是( )

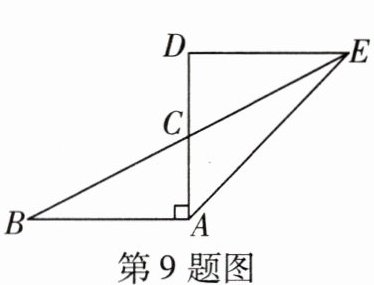
A.1
B.$\sqrt{2}$
C.2
D.$2\sqrt{2}$

答案： D
∵△DEC与△ABC关于点C中心对称，
∴△ABC≌△DEC，
∴DE=AB=2，DC=AC=1，∠D=∠BAC=90°，
∵AD=2，
∴AE=√(AD²+DE²)= √2²+2²=2√2.

10 如图,已知$\triangle ABC与\triangle CDA$关于点O中心对称,过点O作直线EF分别交AD,BC于点E,F,给出下列结论：①点E与点F、点B与点D分别是关于点O的对称点；②直线BD必经过点O；③四边形DEOC与四边形BFOA的面积相等；④$\triangle AOE与\triangle COF$关于点O中心对称. 其中正确的结论是____.(填序号)

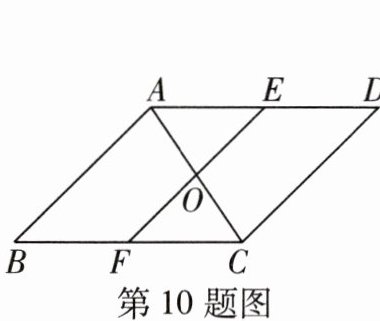
答案： ①②③④

11 [2024广元期末]在如图所示的平面直角坐标系中,$\triangle OA_{1}B_{1}$是边长为2的等边三角形,作$\triangle B_{2}A_{2}B_{1}与\triangle OA_{1}B_{1}关于点B_{1}$中心对称,再作$\triangle B_{2}A_{3}B_{3}与\triangle B_{2}A_{2}B_{1}关于点B_{2}$中心对称,…,如此作下去,则$\triangle B_{2024}A_{2025}B_{2025}的顶点A_{2025}$的坐标是____.

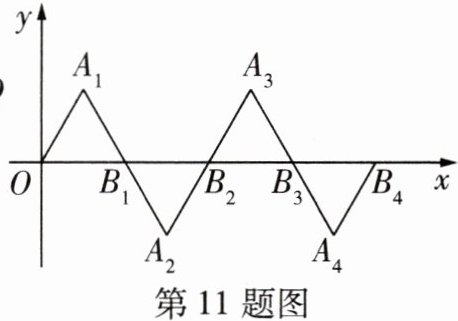
答案： (4049，√3)
∵△OA₁B₁是边长为2的等边三角形，
∴点A₁的坐标为(1，√3)，点B₁的坐标为(2，0).
∵△B₂A₂B₁与△OA₁B₁关于点B₁中心对称，
∴点A₂与点A₁关于点B₁中心对称，
∵2×2-1=3，2×0-√3=-√3，
∴点A₂的坐标是(3，-√3)，
∵△B₂A₃B₃与△B₂A₂B₁关于点B₂中心对称，
∴点A₃与点A₂关于点B₂中心对称，
∵2×3-1=5，2×0-(-√3)=√3，
∴点A₃的坐标是(5，√3)，
∵△B₃A₄B₄与△B₃A₃B₂关于点B₃中心对称，
∴点A₄与点A₃关于点B₃中心对称，
∵2×4-1=7，2×0-√3=-√3，
∴点A₄ 的坐标是(7，-√3)，…，
∵1=2×1-1，3=2×2-1，5=2×3-1，7=2×4-1，…，
∴点Aₙ的横坐标是2n-1，
∴点A₂₀₂₅的横坐标是2×2025-1=4049，
∵当n为奇数时，点Aₙ的纵坐标是√3，当n为偶数时，点Aₙ的纵坐标是-√3，
∴点A₂₀₂₅的纵坐标是√3，即A₂₀₂₅(4049，√3).

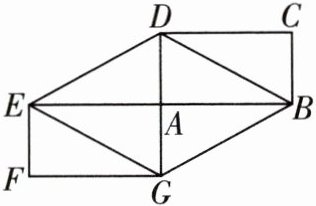
12 [2025陇南期中]如图,矩形ABCD和矩形AEFG关于点A中心对称.
(1)四边形BDEG是菱形吗？请说明理由.
(2)若矩形ABCD的面积为6,求四边形BDEG的面积.

答案： 解：
(1)四边形BDEG是菱形.理由如下：
∵矩形ABCD和矩形AEFG关于点A成中心对称，
∴AB=AE，AD=AG，
∵∠BAE=∠DAG=180°，
∴四边形BDEG是平行四边形，
又∠BAD=90°，
∴BE⊥DG，
∴四边形BDEG是菱形.
(2)
∵矩形ABCD的面积为6，
∴AD×AB=6，
∴S菱形BDEG=1/2×BE×DG=1/2×2AB×2AD=12.

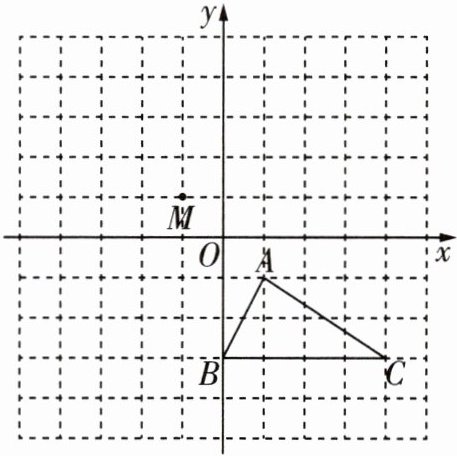
13 新趋势·结论开放[2024宿州期末]如图,在小正方形组成的网格中,$\triangle ABC$的顶点都在格点上,点A的坐标为$(1,-1)$,根据图形解决下列问题.
(1)将$\triangle ABC$先向左平移2个单位长度,再向上平移4个单位长度,得到$\triangle A_{1}B_{1}C_{1}$,请画出$\triangle A_{1}B_{1}C_{1}$.
(2)以点$M(-1,1)$为对称中心,画出与$\triangle A_{1}B_{1}C_{1}中心对称的\triangle A_{2}B_{2}C_{2}$.
(3)如何平移$\triangle ABC$,使得平移后的$\triangle ABC与\triangle A_{2}B_{2}C_{2}$拼成一个平行四边形？请写出一种平移方法.

答案：
解：
(1)如图，△A₁B₁C₁即为所求.

(2)如图，△A₂B₂C₂即为所求.

(3)如图，可将△ABC先向左平移1个单位，再向上平移2个单位，平移后的△ABC与△A₂B₂C₂拼成一个平行四边形.(或将△ABC先向左平移5个单位，再向上平移2个单位；或将△ABC先向左平移4个单位，再向上平移4个单位.答案不唯一)