第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 教材P101T6变式 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P= 50°。则∠BAC的度数为( )
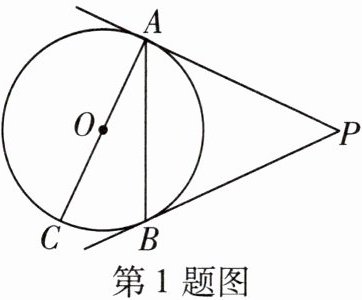
A.20°
B.25°
C.30°
D.35°

A.20°
B.25°
C.30°
D.35°
答案:
B
∵PA,PB 是⊙O 的切线,
∴AP=BP.
∵∠P=50°,
∴∠PAB= $\frac{1}{2}$×(180°-50°)=65°.
∵AC 是⊙O 的直径,
∴∠PAC=90°,
∴∠BAC=90°-65°=25°.
∵PA,PB 是⊙O 的切线,
∴AP=BP.
∵∠P=50°,
∴∠PAB= $\frac{1}{2}$×(180°-50°)=65°.
∵AC 是⊙O 的直径,
∴∠PAC=90°,
∴∠BAC=90°-65°=25°.
2 [2025大连期中]如图,AB,AC,BD是⊙O的切线,切点分别是P,C,D。若AB= 10,AC= 6,则BD的长是( )
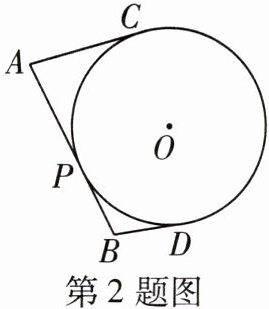
A.3
B.4
C.5
D.6

A.3
B.4
C.5
D.6
答案:
B
∵AC,AP 为⊙O 的切线,
∴AC=AP=6.
∵BP,BD 为⊙O 的切线,
∴BD=BP=AB-AP=10-6=4.
∵AC,AP 为⊙O 的切线,
∴AC=AP=6.
∵BP,BD 为⊙O 的切线,
∴BD=BP=AB-AP=10-6=4.
3 [2025钦州一中期中]如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,且分别交PA,PB于点C,D。若PA= 6,则△PCD的周长为( )
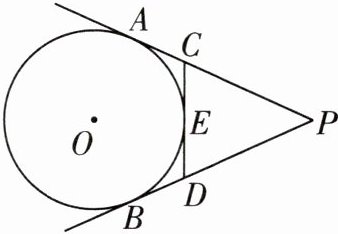
A.5
B.7
C.12
D.10

A.5
B.7
C.12
D.10
答案:
C
∵PA,PB 分别切⊙O 于点 A,B,CD 切⊙O 于点 E,PA=6,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD 的周长为PC+CE+PD+DE=PC+CA+PD+DB=PA+PB=12.
∵PA,PB 分别切⊙O 于点 A,B,CD 切⊙O 于点 E,PA=6,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD 的周长为PC+CE+PD+DE=PC+CA+PD+DB=PA+PB=12.
4 教材P102T11变式 [2025邯郸期中]如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB//CD,OB= 6,OC= 8。
(1)求∠BOC的度数;
(2)求⊙O的半径。
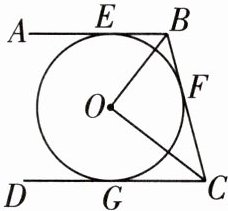
(1)求∠BOC的度数;
(2)求⊙O的半径。
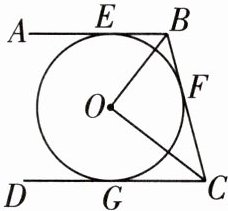
答案:
(1)
∵AB,BC,CD 分别与⊙O 相切于点 E,F,G,
∴∠OBF=∠OBE,∠OCF=∠OCG.
∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF= $\frac{1}{2}$(∠ABC+∠BCD)=90°,
∴∠BOC=90°.
(2)如图,连接 OF,则 OF⊥BC.由
(1)知∠BOC=90°,
∴BC= $\sqrt{OB^2+OC^2}$=10.
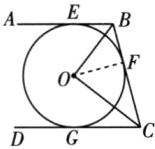
∵$S_{\triangle BOC}$= $\frac{1}{2}$OB·OC= $\frac{1}{2}$BC·OF,
∴OF= $\frac{24}{5}$.即⊙O 的半径为 $\frac{24}{5}$.
(1)
∵AB,BC,CD 分别与⊙O 相切于点 E,F,G,
∴∠OBF=∠OBE,∠OCF=∠OCG.
∵AB//CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF= $\frac{1}{2}$(∠ABC+∠BCD)=90°,
∴∠BOC=90°.
(2)如图,连接 OF,则 OF⊥BC.由
(1)知∠BOC=90°,
∴BC= $\sqrt{OB^2+OC^2}$=10.

∵$S_{\triangle BOC}$= $\frac{1}{2}$OB·OC= $\frac{1}{2}$BC·OF,
∴OF= $\frac{24}{5}$.即⊙O 的半径为 $\frac{24}{5}$.
5 教材P100T1变式 [2024滨州滨城区期中]如图,点I是△ABC的内心,∠BIC= 130°,则∠BAC= ( )
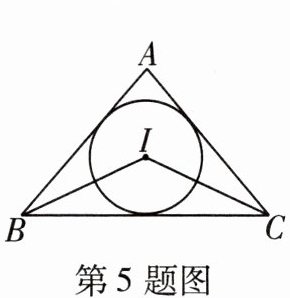
A.60°
B.65°
C.70°
D.80°

A.60°
B.65°
C.70°
D.80°
答案:
D
∵点 I 是△ABC 的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB.
∵∠BIC=130°,
∴∠IBC+∠ICB=180°-∠BIC=50°,
∴∠ABC+∠ACB=2(∠IBC+∠ICB)=100°,
∴∠BAC=180°-(∠ABC+∠ACB)=80°.
∵点 I 是△ABC 的内心,
∴∠ABC=2∠IBC,∠ACB=2∠ICB.
∵∠BIC=130°,
∴∠IBC+∠ICB=180°-∠BIC=50°,
∴∠ABC+∠ACB=2(∠IBC+∠ICB)=100°,
∴∠BAC=180°-(∠ABC+∠ACB)=80°.
6 [2025大连期中]如图,△ABC与它的内切圆⊙O分别相切于点D,E,F。若△ABC的周长为20,BC= 6,则AD的长为( )
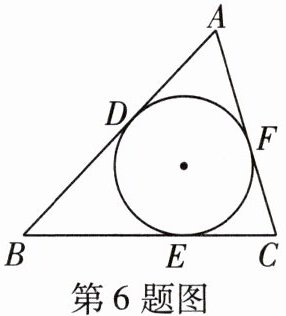
A.8
B.6
C.4
D.5

A.8
B.6
C.4
D.5
答案:
C 设 AD=a.
∵△ABC 与它的内切圆⊙O 分别相切于点D,E,F,
∴AD=AF=a,CE=CF,BE=BD,则 BD+CF=BE+CE=BD=6.
∵△ABC 的周长为20,
∴AD+AF+BD+CF+BC=20,即a+a+6+6=20,解得a=4,即 AD=4.
∵△ABC 与它的内切圆⊙O 分别相切于点D,E,F,
∴AD=AF=a,CE=CF,BE=BD,则 BD+CF=BE+CE=BD=6.
∵△ABC 的周长为20,
∴AD+AF+BD+CF+BC=20,即a+a+6+6=20,解得a=4,即 AD=4.
7 [2024天津河西区期末]一个等边三角形的边长为2,则这个等边三角形的内切圆半径为______。
答案:
$\frac{\sqrt{3}}{3}$ 如图,连接 OA,OB,过点 O 作 OD⊥AB,则 AD= $\frac{1}{2}$AB=1,
∵⊙O 是三角形 ABC 的内切圆,
∴∠OAD=30°,
∴OA=2OD.在Rt△ADO 中,由勾股定理,得$OD^2+AD^2=OA^2$,即$OD^2+1=4OD^2$,所以 OD= $\frac{\sqrt{3}}{3}$.

$\frac{\sqrt{3}}{3}$ 如图,连接 OA,OB,过点 O 作 OD⊥AB,则 AD= $\frac{1}{2}$AB=1,
∵⊙O 是三角形 ABC 的内切圆,
∴∠OAD=30°,
∴OA=2OD.在Rt△ADO 中,由勾股定理,得$OD^2+AD^2=OA^2$,即$OD^2+1=4OD^2$,所以 OD= $\frac{\sqrt{3}}{3}$.

8 如图,已知△ABC,∠B= 40°。
(1)在图中,用尺规作出△ABC的内切圆⊙O,并标出⊙O与边AB,BC,AC的切点D,E,F;(保留作图痕迹,不写作法)
(2)连接EF,DF,求∠EFD的度数。
(1)在图中,用尺规作出△ABC的内切圆⊙O,并标出⊙O与边AB,BC,AC的切点D,E,F;(保留作图痕迹,不写作法)
(2)连接EF,DF,求∠EFD的度数。

答案:
(1)△ABC 的内切圆⊙O 如图所示.
(2)如图,连接 OD,OE.由题意,知 OD⊥AB,OE⊥BC,
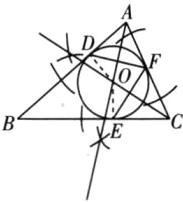
∴∠ODB=∠OEB=90°.
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD= $\frac{1}{2}$∠DOE=70°.
名师点睛 三角形的内切圆的作法 作三角形任意两个内角的平分线,以两条角平分线的交点为圆心,以交点到三角形一边的距离为半径作圆即可.
(1)△ABC 的内切圆⊙O 如图所示.
(2)如图,连接 OD,OE.由题意,知 OD⊥AB,OE⊥BC,

∴∠ODB=∠OEB=90°.
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD= $\frac{1}{2}$∠DOE=70°.
名师点睛 三角形的内切圆的作法 作三角形任意两个内角的平分线,以两条角平分线的交点为圆心,以交点到三角形一边的距离为半径作圆即可.
查看更多完整答案,请扫码查看


