第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2024 德州中考]把多项式$x^{2}-3x+4$进行配方,结果为 ( )
A.$(x-3)^{2}-5$
B.$(x-\frac {3}{2})^{2}+\frac {7}{4}$
C.$(x-\frac {3}{2})^{2}+\frac {25}{4}$
D.$(x+\frac {3}{2})^{2}+\frac {7}{4}$
A.$(x-3)^{2}-5$
B.$(x-\frac {3}{2})^{2}+\frac {7}{4}$
C.$(x-\frac {3}{2})^{2}+\frac {25}{4}$
D.$(x+\frac {3}{2})^{2}+\frac {7}{4}$
答案:
B $x^{2}-3x+4=x^{2}-3x+\frac {9}{4}-\frac {9}{4}+4=(x-\frac {3}{2})^{2}+\frac {7}{4}$.
2 教材 P9T1 变式 填空:
(1)$x^{2}+6x+$____$=(x+$____$)^{2};$
(2)$x^{2}-4x+$____$=(x-$____$)^{2};$
(3)$x^{2}+\frac {2}{5}x+$____$=(x+$____$)^{2};$
(4)$x^{2}-5x+$____$=(x-$____$)^{2}.$
(1)$x^{2}+6x+$____$=(x+$____$)^{2};$
(2)$x^{2}-4x+$____$=(x-$____$)^{2};$
(3)$x^{2}+\frac {2}{5}x+$____$=(x+$____$)^{2};$
(4)$x^{2}-5x+$____$=(x-$____$)^{2}.$
答案:
(1)9 3;
(2)4 2;
(3)$\frac {1}{25}$ $\frac {1}{5}$;
(4)$\frac {25}{4}$ $\frac {5}{2}$
(1)9 3;
(2)4 2;
(3)$\frac {1}{25}$ $\frac {1}{5}$;
(4)$\frac {25}{4}$ $\frac {5}{2}$
3 [2025 沈阳浑南区期末]用配方法解方程$x^{2}+x= 2$时,应把方程的两边同时 ( )
A.加$\frac {1}{4}$
B.加$\frac {1}{2}$
C.减$\frac {1}{4}$
D.减$\frac {1}{2}$
A.加$\frac {1}{4}$
B.加$\frac {1}{2}$
C.减$\frac {1}{4}$
D.减$\frac {1}{2}$
答案:
A
4 [2023 赤峰中考]用配方法解方程$x^{2}-4x-1= 0$时,配方后正确的是 ( )
A.$(x+2)^{2}= 3$
B.$(x+2)^{2}= 17$
C.$(x-2)^{2}= 5$
D.$(x-2)^{2}= 17$
A.$(x+2)^{2}= 3$
B.$(x+2)^{2}= 17$
C.$(x-2)^{2}= 5$
D.$(x-2)^{2}= 17$
答案:
C $x^{2}-4x-1=0$,移项,得$x^{2}-4x=1$.配方,得$x^{2}-4x+4=1+4$,即$(x-2)^{2}=5$.
5 [2025 海口期末]将一元二次方程$x^{2}-6x-4= 0化成(x+a)^{2}= b$的形式,则b的值为 ( )
A.3
B.4
C.7
D.13
A.3
B.4
C.7
D.13
答案:
D 把方程$x^{2}-6x-4=0$的常数项移到等号的右边,得$x^{2}-6x=4$,方程两边同时加上一次项系数一半的平方,得$x^{2}-6x+9=4+9$,配方得$(x-3)^{2}=13$,故$b=13$.
6 新趋势·过程性学习[2025 石家庄四十一中月考]老师设计了接力游戏,用合作的方式完成配方法解一元二次方程,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后解出方程.过程如图所示,接力中,自己负责的一步出现错误的是( )
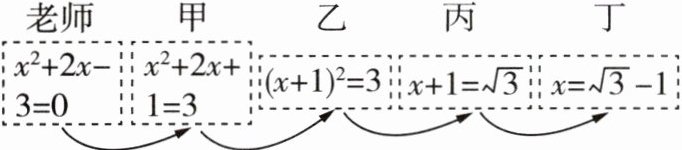
A.只有甲
B.甲和乙
C.甲和丙
D.丙和丁
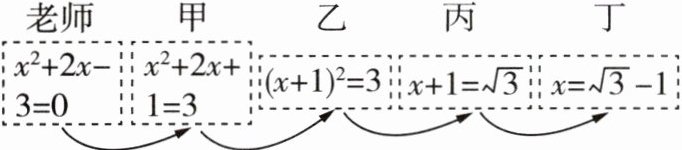
A.只有甲
B.甲和乙
C.甲和丙
D.丙和丁
答案:
C $x^{2}+2x-3=0→x^{2}+2x+1=3+1$(易错点:方程两边同时加上一次项系数一半的平方,勿忘等号右边)→$(x+1)^{2}=4→x+1=\pm 2→x+1=2$或$x+1=-2→x_{1}=1,x_{2}=-3$,
∴ 接力中,自己负责的一步出现错误的是甲和丙.
∴ 接力中,自己负责的一步出现错误的是甲和丙.
7 用配方法解下列方程:
(1)$x^{2}-2x= 5;$
(2)$x(x+7)= 4x-1.$
(1)$x^{2}-2x= 5;$
(2)$x(x+7)= 4x-1.$
答案:
解:
(1)配方,得$x^{2}-2x+1=5+1$,即$(x-1)^{2}=6$.由此可得$x-1=\pm \sqrt {6}$,
∴$x_{1}=1+\sqrt {6},x_{2}=1-\sqrt {6}$.
(2)原方程可化为$x^{2}+3x=-1$.配方,得$x^{2}+3x+\frac {9}{4}=-1+\frac {9}{4}$,即$(x+\frac {3}{2})^{2}=\frac {5}{4}$.由此可得$x+\frac {3}{2}=\pm \frac {\sqrt {5}}{2}$,
∴$x_{1}=\frac {\sqrt {5}}{2}-\frac {3}{2},x_{2}=-\frac {\sqrt {5}}{2}-\frac {3}{2}$.
(1)配方,得$x^{2}-2x+1=5+1$,即$(x-1)^{2}=6$.由此可得$x-1=\pm \sqrt {6}$,
∴$x_{1}=1+\sqrt {6},x_{2}=1-\sqrt {6}$.
(2)原方程可化为$x^{2}+3x=-1$.配方,得$x^{2}+3x+\frac {9}{4}=-1+\frac {9}{4}$,即$(x+\frac {3}{2})^{2}=\frac {5}{4}$.由此可得$x+\frac {3}{2}=\pm \frac {\sqrt {5}}{2}$,
∴$x_{1}=\frac {\sqrt {5}}{2}-\frac {3}{2},x_{2}=-\frac {\sqrt {5}}{2}-\frac {3}{2}$.
8 下面是用配方法解关于x的一元二次方程$3x^{2}+2x-1= 0$的具体过程.
解:第一步:$x^{2}+\frac {2}{3}x-\frac {1}{3}= 0.$
第二步:$x^{2}+\frac {2}{3}x= \frac {1}{3}.$
第三步:$x^{2}+\frac {2}{3}x+(\frac {1}{3})^{2}= \frac {1}{3}+(\frac {1}{3})^{2}.$
第四步:$(x+\frac {1}{3})^{2}= \frac {4}{9},\therefore x+\frac {1}{3}= \pm \frac {2}{3},\therefore x_{1}= \frac {1}{3},x_{2}= -1.$
以下四条语句与上面四步对应:①移项:方程左边为二次项和一次项,右边为常数项;②求解:用直接开平方法解一元二次方程;③配方:根据完全平方公式,在方程的两边各加上一次项系数一半的平方;④二次项系数化1,方程两边都除以二次项系数.则第一步、第二步、第三步、第四步应对应的语句分别是____.
解:第一步:$x^{2}+\frac {2}{3}x-\frac {1}{3}= 0.$
第二步:$x^{2}+\frac {2}{3}x= \frac {1}{3}.$
第三步:$x^{2}+\frac {2}{3}x+(\frac {1}{3})^{2}= \frac {1}{3}+(\frac {1}{3})^{2}.$
第四步:$(x+\frac {1}{3})^{2}= \frac {4}{9},\therefore x+\frac {1}{3}= \pm \frac {2}{3},\therefore x_{1}= \frac {1}{3},x_{2}= -1.$
以下四条语句与上面四步对应:①移项:方程左边为二次项和一次项,右边为常数项;②求解:用直接开平方法解一元二次方程;③配方:根据完全平方公式,在方程的两边各加上一次项系数一半的平方;④二次项系数化1,方程两边都除以二次项系数.则第一步、第二步、第三步、第四步应对应的语句分别是____.
答案:
④①③②
9 教材 P9T2 变式 用配方法解下列方程:
(1)$2x^{2}-3= 4x;$
(2)$\frac {1}{2}x^{2}-6x-7= 0.$
(1)$2x^{2}-3= 4x;$
(2)$\frac {1}{2}x^{2}-6x-7= 0.$
答案:
解:
(1)原方程可化为$2x^{2}-4x=3$.二次项系数化为1,得$x^{2}-2x=\frac {3}{2}$.配方,得$x^{2}-2x+1=\frac {3}{2}+1$,即$(x-1)^{2}=\frac {5}{2}$.由此可得$x-1=\frac {\sqrt {10}}{2}$或$x-1=-\frac {\sqrt {10}}{2}$,
∴$x_{1}=1+\frac {\sqrt {10}}{2},x_{2}=1-\frac {\sqrt {10}}{2}$.
(2)移项,得$\frac {1}{2}x^{2}-6x=7$.二次项系数化为1,得$x^{2}-12x=14$.配方,得$x^{2}-12x+36=14+36$,即$(x-6)^{2}=50$.由此可得$x-6=5\sqrt {2}$或$x-6=-5\sqrt {2}$,
∴$x_{1}=6+5\sqrt {2},x_{2}=6-5\sqrt {2}$.
(1)原方程可化为$2x^{2}-4x=3$.二次项系数化为1,得$x^{2}-2x=\frac {3}{2}$.配方,得$x^{2}-2x+1=\frac {3}{2}+1$,即$(x-1)^{2}=\frac {5}{2}$.由此可得$x-1=\frac {\sqrt {10}}{2}$或$x-1=-\frac {\sqrt {10}}{2}$,
∴$x_{1}=1+\frac {\sqrt {10}}{2},x_{2}=1-\frac {\sqrt {10}}{2}$.
(2)移项,得$\frac {1}{2}x^{2}-6x=7$.二次项系数化为1,得$x^{2}-12x=14$.配方,得$x^{2}-12x+36=14+36$,即$(x-6)^{2}=50$.由此可得$x-6=5\sqrt {2}$或$x-6=-5\sqrt {2}$,
∴$x_{1}=6+5\sqrt {2},x_{2}=6-5\sqrt {2}$.
查看更多完整答案,请扫码查看


