《2025年一遍过九年级初中数学上册人教版》

9 [2023聊城中考]如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA。若∠CAI= 35°,则∠OBC的度数为( )

A.15°
B.17.5°
C.20°
D.25°

答案：
C 如图,连接 OC.
∵点 I 是△ABC 的内心,
∴AI 平分∠BAC.
∵∠CAI=35°,
∴∠BAC=2∠CAI=70°.
∵点 O 是△ABC 外接圆的圆心,
∴∠BOC=2∠BAC=140°.
∵OB=OC,
∴∠OBC=∠OCB= $\frac{1}{2}$×(180°-∠BOC)= $\frac{1}{2}$×(180°-140°)=20°.

10 [2024泸州中考]如图,EA,ED是⊙O的切线,切点分别为A,D,点B,C在⊙O上,若∠BAE+∠BCD= 236°,则∠E= ( )

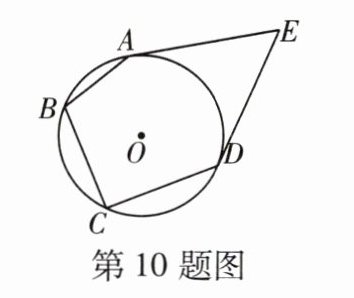
A.56°
B.60°
C.68°
D.70°

答案：
C 如图,连接 AD.
∵四边形 ABCD 是⊙O 的内接四边形,
∴∠BAD+∠BCD=180°.
∵∠BAE+∠BCD=236°,
∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°,
∴∠EAD=56°.
∵EA,ED 是⊙O 的切线,切点为 A,D,
∴EA=ED,
∴∠EDA=∠EAD=56°,
∴∠E=180°-∠EDA-∠EAD=180°-56°-56°=68°.

11 一题多解 [2024滨州中考]刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”。刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式。如图,Rt△ABC中,∠C= 90°,AB,BC,CA的长分别为c,a,b。则可以用含c,a,b的式子表示出△ABC的内切圆直径d,下列表达式错误的是( )

A.d= a+b-c

B.d= $\frac{2ab}{a+b+c}$
C.d= $\sqrt{2(c-a)(c-b)}$
D.d= |(a-b)(c-b)|

答案：
D 优解(特殊值法)
∵三角形 ABC 为直角三角形,
∴令a=3,b=4,c=5.选项 A:d=a+b-c=2.选项 B:d= $\frac{2ab}{a+b+c}$=2.选项 C:d= $\sqrt{2(c-a)(c-b)}$=2.选项 D:d=|(a-b)(c-b)|=1,很明显,只有 D 选项跟其他选项不一致,
∴表达式错误的应是 D 选项.
通解 如图,作 OE⊥AC 于点 E,OD⊥BC 于点 D,OF⊥AB 于点 F.易证四边形 OECD 是正方形,设 OE=OD=OF=r,则EC=CD=r,
∴AE=AF=b-r,BD=BF=a-r.
∵AF+BF=AB,
∴b-r+a-r=c,
∴r= $\frac{a+b-c}{2}$,
∴d=a+b-c.故选项 A正确.
∵$S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle BOC}+S_{\triangle AOB}$,
∴$\frac{1}{2}ab=\frac{1}{2}ar+\frac{1}{2}br+\frac{1}{2}cr$,
∴ab=r(a+b+c),
∴r= $\frac{ab}{a+b+c}$,即 d= $\frac{2ab}{a+b+c}$.故选项 B 正确.
∵由前面可知 d=a+b-c,
∴$d^2=(a+b-c)^2=(a+b)^2-2c(a+b)+c^2=a^2+2ab+b^2-2ac-2bc+c^2$.
∵$a^2+b^2=c^2$,
∴$d^2=2c^2+2ab-2ac-2bc=2(c^2+ab-ac-bc)=2[(c^2-ac)+b(a-c)]=2(c-a)(c-b)$,
∴d= $\sqrt{2(c-a)(c-b)}$,故选项 C 正确.

12 [2025长沙南雅中学月考]如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,给出下列结论：①∠BAD= ∠CAD；②若点G为BC的中点,则∠BGD= 90°；③连接BE,CE,若∠BAC= 40°,则∠BEC= 140°；④BD= DE。其中正确结论的个数是( )

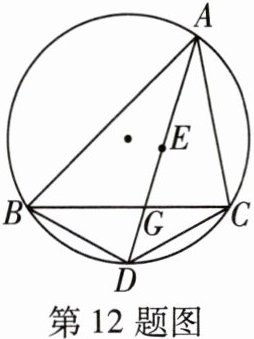
A.4
B.3
C.2
D.1

答案：
B
∵点 E 是△ABC 的内心,
∴AD 平分∠BAC,
∴∠BAD=∠CAD,故①正确.设△ABC 的外接圆圆心为 O,连接 OD,则OD 垂直平分 BC.
∵点 G 为 BC 的中点,
∴点 G 为 OD 与 BC 的交点,即∠BGD=90°,故②正确.
∵∠BAC=40°,
∴∠ABC+∠ACB=180°-∠BAC=140°.
∵点 E 是△ABC 的内心,
∴∠EBC=∠ABE= $\frac{1}{2}$∠ABC,∠ECB=∠ACE= $\frac{1}{2}$∠ACB,
∴∠BEC=180°-(∠EBC+∠ECB)=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$×140°=110°,故③错误.
∵∠BAD=∠CAD,
∴$\widehat{BD}=\widehat{CD}$,
∴∠DBC=∠BAD.
∵∠DBE=∠DBC+∠EBC,∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB,
∴BD=DE,故④正确.综上,正确的结论有 3 个.

13 [2025盘锦双子台区期中]如图,点O为△ABC的内心,将∠ABC平移使顶点B与点O重合,两边与AC分别交于点D,E,若AB= 5,BC= 4,AC= 7,则△ODE的周长是______。

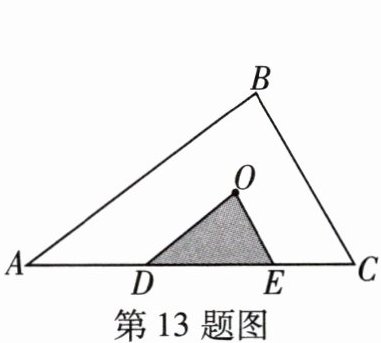
答案：
7

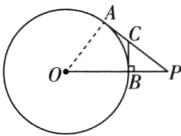
14 如图,点P为⊙O外一点,PA与⊙O相切于点A,PO交⊙O于点B,BC⊥OP交PA于点C,BC= 3,PB= 4,求⊙O的半径。

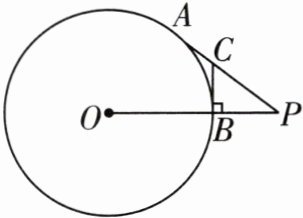
答案：
如图,连接 OA.
∵OB⊥BC,OB 是⊙O 的半径,
∴BC 是⊙O 的切线.

∵PA 与⊙O 相切于点 A,
∴CA=CB=3,∠OAP=90°.在 Rt△PBC 中,由勾股定理,得 PC= $\sqrt{BC^2+BP^2}$=5,
∴AP=CA+PC=8.设⊙O 的半径为 r,则 OP=r+4.在 Rt△AOP 中,由勾股定理,得$OA^2+AP^2=OP^2$,
∴$r^2+8^2=(r+4)^2$,解得 r=6,
∴⊙O 的半径为 6.

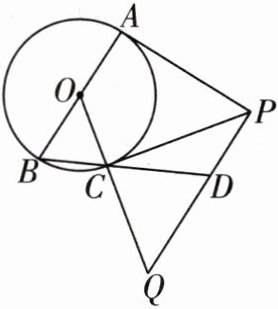
15 推理能力 如图,AB为⊙O的直径,PA,PC分别与⊙O相切于点A,C,PQ⊥PA交OC的延长线于点Q。
(1)求证：OQ= PQ。
(2)连接BC并延长,交PQ于点D,PA= AB,且CQ= 6,求BD的长。

答案：

(1)证明:如图,连接 OP.
∵PA,PC 分别与⊙O 相切于点 A,C,

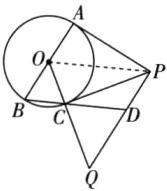
∴PA=PC,OA⊥PA,OC⊥PC,易证△OPA≌△OPC,
∴∠AOP=∠COP.
∵PQ⊥PA,
∴PQ//AB,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)解:设 OA=r.
∵OB=OC,
∴∠OBC=∠OCB.
∵OB//QD,
∴∠QDC=∠OBC,
∴∠OCB=∠QDC.
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QD=QC=6.由
(1)知 OQ=PQ,
∴DP=OC=r,
∴PQ=QD+DP=6+r.
∵PA=PC,PA=AB,
∴PC=AB=2r.
∵PC 是⊙O 的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°.在 Rt△PCQ 中,$PQ^2=PC^2+QC^2$,
∴$(6+r)^2=(2r)^2+6^2$,解得 r=4(0 舍去),
∴OA=4,PA=8,
∴在 Rt△AOP 中,OP= $\sqrt{OA^2+PA^2}=\sqrt{4^2+8^2}=4\sqrt{5}$.
∵OB=PD,OB//PD,
∴四边形 OBDP 是平行四边形,
∴BD=OP=4$\sqrt{5}$.