第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2025吕梁兴县多校月考]【阅读与思考】
下面是博学小组研究性学习报告的部分内容.请认真阅读并解答下列问题.
过圆外一点作圆的切线的尺规作图.
已知:如图1,$\odot O及圆外一点P$.
求作:过点$P作\odot O$的一条切线.
作法:①连接$OP$;
②作$OP$的______,交$OP于点A$;
③以点$A$为圆心,$OA长为半径作\odot A$,交$\odot O于点B$;
④作直线$PB$.
直线$PB$即为所求作的一条切线.
(1)直接写出研究性学习报告空缺的内容:______.
(2)求证:直线$PB为\odot O$的切线.
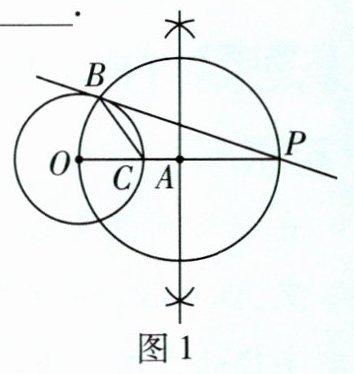
(3)如图1,$C为OA与\odot O$的交点,连接$BC$.若$∠BPO= 20^{\circ }$,则$∠BCO= $______$^{\circ }$.
(4)拓展小组也给出了作法:如图2,连接$OP交\odot O于点C$,过点$C作OP的垂线n$,以点$O$为圆心,$OP$长为半径作弧,交直线$n于点D$,连接$OD交\odot O于点B$,作直线$BP$,则直线$BP$即为所求作的切线.
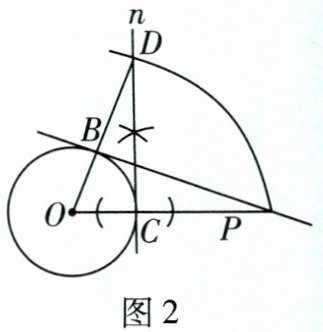
问题:请你结合该组作图方案给出证明过程.
【追问】(5)你是否还有其他方法用尺规作出过圆外一点作圆的切线.
下面是博学小组研究性学习报告的部分内容.请认真阅读并解答下列问题.
过圆外一点作圆的切线的尺规作图.
已知:如图1,$\odot O及圆外一点P$.
求作:过点$P作\odot O$的一条切线.
作法:①连接$OP$;
②作$OP$的______,交$OP于点A$;
③以点$A$为圆心,$OA长为半径作\odot A$,交$\odot O于点B$;
④作直线$PB$.
直线$PB$即为所求作的一条切线.
(1)直接写出研究性学习报告空缺的内容:______.
(2)求证:直线$PB为\odot O$的切线.

(3)如图1,$C为OA与\odot O$的交点,连接$BC$.若$∠BPO= 20^{\circ }$,则$∠BCO= $______$^{\circ }$.
(4)拓展小组也给出了作法:如图2,连接$OP交\odot O于点C$,过点$C作OP的垂线n$,以点$O$为圆心,$OP$长为半径作弧,交直线$n于点D$,连接$OD交\odot O于点B$,作直线$BP$,则直线$BP$即为所求作的切线.

问题:请你结合该组作图方案给出证明过程.
【追问】(5)你是否还有其他方法用尺规作出过圆外一点作圆的切线.
答案:
(1)解:垂直平分线
(2)证明:连接OB.
∵OP为⊙O的直径,
∴∠OBP=90°,
∴PB⊥OB,
∵OB是⊙O的半径,
∴直线PB为⊙O的切线.
(3)解:55
在Rt△BOP中,∠BOP=90° - ∠BPO=70°,在△OBC中,CO=
OB,则∠BCO=$\frac{1}{2}$(180° - ∠BOP)=$\frac{1}{2}$×(180° - 70°)=55°.
(4)证明:由作图知,CD⊥OP于点C,OP=OD,OB=OC,
∴∠OCD=90°,
又
∵∠DOC=∠POB,
∴△OBP≌△OCD(SAS),
∴∠OBP=∠OCD=90°,即PB⊥OB.
又
∵OB是⊙O的半径,
∴PB是⊙O的切线.
(5)解:如图,连接OP,交⊙O于点B,作直径BC,以点O为圆心,BC长为半径作弧;以P为圆心,OP长为半径作弧,两弧相交于点D,连接OD,交⊙O于点M,作直线PM.直线PM即为所求.

(1)解:垂直平分线
(2)证明:连接OB.
∵OP为⊙O的直径,
∴∠OBP=90°,
∴PB⊥OB,
∵OB是⊙O的半径,
∴直线PB为⊙O的切线.
(3)解:55
在Rt△BOP中,∠BOP=90° - ∠BPO=70°,在△OBC中,CO=
OB,则∠BCO=$\frac{1}{2}$(180° - ∠BOP)=$\frac{1}{2}$×(180° - 70°)=55°.
(4)证明:由作图知,CD⊥OP于点C,OP=OD,OB=OC,
∴∠OCD=90°,
又
∵∠DOC=∠POB,
∴△OBP≌△OCD(SAS),
∴∠OBP=∠OCD=90°,即PB⊥OB.
又
∵OB是⊙O的半径,
∴PB是⊙O的切线.
(5)解:如图,连接OP,交⊙O于点B,作直径BC,以点O为圆心,BC长为半径作弧;以P为圆心,OP长为半径作弧,两弧相交于点D,连接OD,交⊙O于点M,作直线PM.直线PM即为所求.

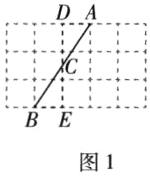
2 [2024扬州仪征期中]【经历】(1)如图1所示的正方形网格中,每个小的四边形都是相同的正方形,$A,B$都是格点,线段$AB交竖直网格线于点C$,则$AC与BC$的数量关系是______.
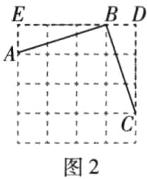
(2)如图2所示的正方形网格中,每个小的四边形都是相同的正方形,$A,B,C$都是格点,则$AB与BC$的位置关系是______.
【体会】网格背景下的画图,它主要是利用网格自身的位置及数量的特殊性,画图时借助网格中的格点,构造一些几何模型,如全等模型、特殊三角形、特殊四边形等,再借助图形的性质解决问题.
【实践】如图3是由小正方形组成的$9×7$网格,每个小正方形的顶点叫做格点,$A,B,C$三个格点都在圆上.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(3)画出该圆的圆心$O$.
(4)画出格点$E$,使$EA为\odot O$的一条切线,并画出过点$E的另一条切线EF$,切点为$F$.

(2)如图2所示的正方形网格中,每个小的四边形都是相同的正方形,$A,B,C$都是格点,则$AB与BC$的位置关系是______.
【体会】网格背景下的画图,它主要是利用网格自身的位置及数量的特殊性,画图时借助网格中的格点,构造一些几何模型,如全等模型、特殊三角形、特殊四边形等,再借助图形的性质解决问题.
【实践】如图3是由小正方形组成的$9×7$网格,每个小正方形的顶点叫做格点,$A,B,C$三个格点都在圆上.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(3)画出该圆的圆心$O$.
(4)画出格点$E$,使$EA为\odot O$的一条切线,并画出过点$E的另一条切线EF$,切点为$F$.

答案:
(1)AC=BC
如图1,
∵AD//BE,
∴∠DAC=∠CBE,∠ADC=∠BEC,
∵AD=
BE,
∴△ADC≌△BEC(ASA),
∴AC=BC.
(2)AB⊥BC
如图2,
∵AE=BD,∠AEB=∠BDC,BE=CD,
∴△ABE≌△BCD(SAS),
∴∠ABE=∠BCD.
∵∠BCD+∠CBD=90°,
∴∠ABE+∠CBD=90°,
∴∠ABC=180° - 90°=90°,
∴AB⊥BC.
(3)解题思路:
∵∠BCD=90°,∠BAD=90°,
∴AC,BD是直径,
∴两直径AC,BD的交点即该圆的圆心O.
如图3,取格点D,连接AC,BD.AC,BD的交点即为圆心O.
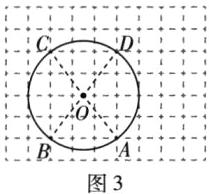
(4)解题思路:由图可得△AHE≌△CBA(SAS),
∴∠CAB=∠AEH,∠BCA=∠EAH,
∵∠EAH+∠AEH=90°,
∴∠EAH+∠CAB=90°,
∴∠CAE=90°,
∴EA为⊙O的一条切线;取格点P,Q交网格线于点J,连接AJ交⊙O于点F,点F与点A关于OE对称,即EF为⊙O的另一条切线.
如图4,直线AE,EF即为所求.

(1)AC=BC
如图1,
∵AD//BE,
∴∠DAC=∠CBE,∠ADC=∠BEC,
∵AD=
BE,
∴△ADC≌△BEC(ASA),
∴AC=BC.

(2)AB⊥BC
如图2,
∵AE=BD,∠AEB=∠BDC,BE=CD,
∴△ABE≌△BCD(SAS),
∴∠ABE=∠BCD.
∵∠BCD+∠CBD=90°,
∴∠ABE+∠CBD=90°,
∴∠ABC=180° - 90°=90°,
∴AB⊥BC.

(3)解题思路:
∵∠BCD=90°,∠BAD=90°,
∴AC,BD是直径,
∴两直径AC,BD的交点即该圆的圆心O.
如图3,取格点D,连接AC,BD.AC,BD的交点即为圆心O.

(4)解题思路:由图可得△AHE≌△CBA(SAS),
∴∠CAB=∠AEH,∠BCA=∠EAH,
∵∠EAH+∠AEH=90°,
∴∠EAH+∠CAB=90°,
∴∠CAE=90°,
∴EA为⊙O的一条切线;取格点P,Q交网格线于点J,连接AJ交⊙O于点F,点F与点A关于OE对称,即EF为⊙O的另一条切线.
如图4,直线AE,EF即为所求.

查看更多完整答案,请扫码查看


