《2025年一遍过九年级初中数学上册人教版》

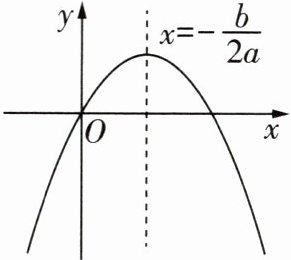
11 [2023河南中考]二次函数$y= ax^{2}+bx$的图象如图所示,则一次函数$y= x+b$的图象一定不经过( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： D
∵抛物线开口向下，
∴ $ a＜0 $.
∵抛物线的对称轴在y轴右侧，
∴ $ -\frac{b}{2a}＞0 $，
∴ $ b＞0 $，
∴ $ y=x + b $ 的图象经过第一、第二、第三象限，不经过第四象限.

12 [2023陕西中考]在平面直角坐标系中,二次函数$y= x^{2}+mx+m^{2}-m$(m为常数)的图象经过点$(0,6)$,其对称轴在y轴左侧,则该二次函数有( )

A.最大值5
B.最大值$\frac {15}{4}$
C.最小值5
D.最小值$\frac {15}{4}$

答案： D 由题意，得 $ 6=m^{2}-m $，解得 $ m_{1}=3,m_{2}=-2 $.
∵二次函数 $ y=x^{2}+mx+m^{2}-m $ 的图象的对称轴在y轴左侧，
∴ $ -\frac{m}{2}＜0 $，
∴ $ m＞0 $，
∴ $ m=3 $，
∴ $ y=x^{2}+3x + 6 $.
∵ $ a=1＞0 $，
∴抛物线开口向上，
∴二次函数有最小值，为 $ \frac{4ac - b^{2}}{4a}=\frac{4×1×6 - 3^{2}}{4×1}=\frac{15}{4} $.

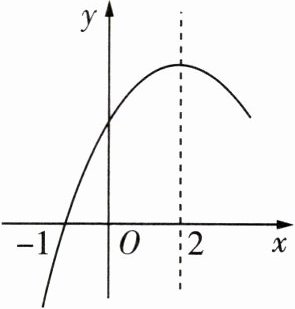
13 [2022广元中考]二次函数$y= ax^{2}+bx+c(a≠0)$的部分图象如图所示,图象过点$(-1,0)$,对称轴为直线$x= 2$,给出下列结论：
(1)$abc＜0$；(2)$4a+c＞2b$；(3)$3b-2c＞0$；(4)若点$A(-2,y_{1})$,点$B(-\frac {1}{2},y_{2})$,点$C(\frac {7}{2},y_{3})$在该函数图象上,则$y_{1}＜y_{3}＜y_{2}$；(5)$4a+2b≥m(am+b)$(m为常数).其中正确的结论有( )
A. 5个
B. 4个
C. 3个
D. 2个

答案： C 序号 分析 结论
(1)
∵二次函数的图象开口向下，
∴ $ a＜0 $.
∵二次函数图象的对称轴为直线 $ x=-\frac{b}{2a}=2 $，
∴ $ b＞0 $.
∵二次函数图象与y轴交于正半轴，
∴ $ c＞0 $，
∴ $ abc＜0 $ 正确
(2) 由题图可知，当 $ x=-2 $ 时， $ y＜0 $，即 $ 4a - 2b + c＜0 $，
∴ $ 4a + c＜2b $ 错误
(3) 由
(1)得 $ -\frac{b}{2a}=2 $，
∴ $ b=-4a $.
∵二次函数图象经过点(-1,0)，
∴ $ a - b + c=0 $，
∴ $ c=b - a=-4a - a=-5a $，
∴ $ 3b - 2c=-12a + 10a=-2a＞0 $ 正确
(4) 二次函数图象开口向下，图象上的点到对称轴的距离越远，函数值越小.
∵ $ |-2 - 2|=4 $， $ |-\frac{1}{2}-2|=\frac{5}{2} $， $ |\frac{7}{2}-2|=\frac{3}{2} $，
∴ $ y_{1}＜y_{2}＜y_{3} $ 错误
(5) 当 $ x=2 $ 时，二次函数有最大值 $ 4a + 2b + c $，
∴ $ 4a + 2b + c\geqslant am^{2}+bm + c $，
∴ $ 4a + 2b\geqslant m(am + b) $(m为常数) 正确

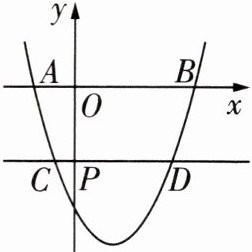
14 [2025杭州余杭区期中]如图,抛物线$y= ax^{2}+bx-3(a≠0)$交x轴于$A(-1,0)$,$B(3,0)$两点.P是y轴上一点,过点P作一条平行于x轴的直线,交该抛物线于C,D两点(点C在左边,点D在右边).若$DP= 4PC$,则点C的横坐标是____.

答案： $\frac{2}{5}$或$-\frac{2}{3}$ 把A(-1,0),B(3,0)的坐标分别代入 $ y=ax^{2}+bx - 3(a≠0) $，得 $ \begin{cases} a - b - 3=0 \\ 9a + 3b - 3=0 \end{cases} $，解得 $ \begin{cases} a=1 \\ b=-2 \end{cases} $，
∴该抛物线的解析式为 $ y=x^{2}-2x - 3=(x - 1)^{2}-4 $，
∴对称轴为直线 $ x=1 $.设C(x,y)，
∵ $ CD// x $ 轴，
∴D(2 - x,y)，P(0,y)，
∴ $ PC=|x| $， $ PD=|2 - x| $，
∵ $ DP=4PC $，
∴ $ |2 - x|=4|x| $，
∴ $ 2 - x=\pm4x $，解得 $ x=\frac{2}{5} $ 或 $ x=-\frac{2}{3} $.

15 [2024北京中考]在平面直角坐标系xOy中,已知抛物线$y= ax^{2}-2a^{2}x(a≠0)$.
(1)当$a= 1$时,求抛物线的顶点坐标；
(2)已知$M(x_{1},y_{1})和N(x_{2},y_{2})$是抛物线上的两点,若对于$x_{1}= 3a$,$3≤x_{2}≤4$,都有$y_{1}＜y_{2}$,求a的取值范围.

答案： 解:
(1)把 $ a=1 $ 代入 $ y=ax^{2}-2a^{2}x $，得 $ y=x^{2}-2x=(x - 1)^{2}-1 $，
∴抛物线的顶点坐标为(1,-1).
(2)抛物线的对称轴为直线 $ x=-\frac{-2a^{2}}{2a}=a $，
∴点 $ M(3a,y_{1}) $ 关于对称轴的对称点为 $ (-a,y_{1}) $.
分两种情况讨论.
①当 $ a＞0 $ 时，如图1.
∵ $ y_{1}＜y_{2} $，
∴点N在点M右侧，即 $ 3a＜3 $，
解得 $ a＜1 $，
∴ $ 0＜a＜1 $.
②当 $ a＜0 $ 时，如图2.
∵ $ y_{1}＜y_{2} $，
∴ $ -a＞4 $ 且 $ 3a＜3 $，解得 $ a＜-4 $.
综上可知，a的取值范围为 $ 0＜a＜1 $ 或 $ a＜-4 $.

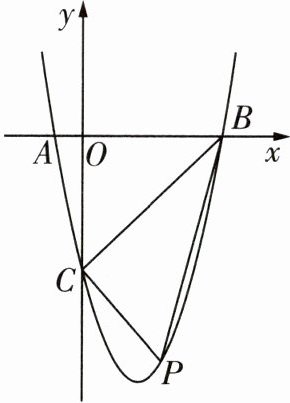
16 [推理能力[2023娄底中考节选]如图,抛物线$y= x^{2}+bx+c过点A(-1,0)$,点$B(5,0)$,交y轴于点C.
(1)求b,c的值.
(2)点$P(x_{0},y_{0})(0＜x_{0}＜5)$是抛物线上的动点.当$x_{0}$取何值时,$\triangle PBC$的面积最大？并求出$\triangle PBC$面积的最大值.

答案： 解:
(1)
∵抛物线 $ y=x^{2}+bx + c $ 过点A(-1,0)，点B(5,0)，
∴ $ \begin{cases} 0=1 - b + c \\ 0=25 + 5b + c \end{cases} $，解得 $ \begin{cases} b=-4 \\ c=-5 \end{cases} $.
(2)由
(1)得，抛物线的解析式为 $ y=x^{2}-4x - 5 $，令 $ x=0 $，则 $ y=-5 $，
∴C(0,-5)，
∴直线BC的解析式为 $ y=x - 5 $.
如图，过点P作x轴的垂线，交线段BC于点D，由 $ P(x_{0},x_{0}^{2}-4x_{0}-5) $，得 $ D(x_{0},x_{0}-5) $，
∴ $ S_{\triangle PBC}=\frac{1}{2}OB\cdot PD=\frac{1}{2}×5×(x_{0}-5 - x_{0}^{2}+4x_{0}+5)=-\frac{5}{2}x_{0}^{2}+\frac{25}{2}x_{0}=-\frac{5}{2}(x_{0}-\frac{5}{2})^{2}+\frac{125}{8} $，
∴当 $ x_{0}=\frac{5}{2} $ 时， $ S_{\triangle PBC} $ 有最大值，最大值为 $ \frac{125}{8} $.