《2025年轻松总复习暑假作业七年级数学》

17. 解方程组:
(1)$\begin{cases}3s - t = 5, & ①\\5s + 2t = 12; & ②\end{cases}$
(2)$\begin{cases}3x + 4y = 16, & ①\\5x - 6y = 33. & ②\end{cases}$

答案： 17. 解:
(1) 由①得, $t = 3s - 5$③, 把③代入②得:
$5s + 6s - 10 = 12$, 解得: $s = 2$, 把 $s = 2$ 代入③得: $t = 1$.
∴ 原方程组的解是 $\begin{cases} s = 2, \\ t = 1. \end{cases}$
(2) ① $× 3$ 得, $9x + 12y = 48$③, ② $× 2$ 得, $10x - 12y = 66$④, ③ + ④得, $19x = 114$, $x = 6$. 将 $x = 6$ 代入①得, $y = -\frac{1}{2}$.
∴ 原方程组的解是 $\begin{cases} x = 6, \\ y = -\frac{1}{2}. \end{cases}$

18. 解一元一次不等式(组):
(1)$3(2x+5)＞2(4x+3);$
(2)$\left\{\begin{array}{l} 3(x+2)≥x+4,\\ \frac {x-1}{2}＜1.\end{array} \right. $

答案： 18.
(1) $x ＜ \frac{9}{2}$;
(2) $-1 \leq x ＜ 3$.

19. 如图所示,已知$AB// DE,BC// EF,∠B= 60^{\circ }$,求$∠E$的度数.

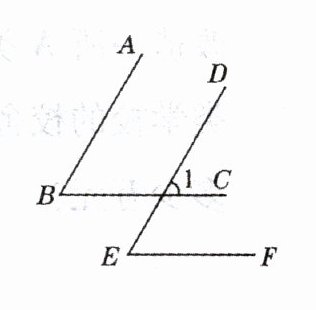
答案： 19. 解: $\because AB // DE$, $BC // EF$ (已知), $\therefore \angle B = \angle 1$, $\angle 1 = \angle E$ (两直线平行, 同位角相等), $\therefore \angle B = \angle E$ (等量代换), 又 $\because \angle B = 60^{\circ}$ (已知), $\therefore \angle E = 60^{\circ}$.