《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

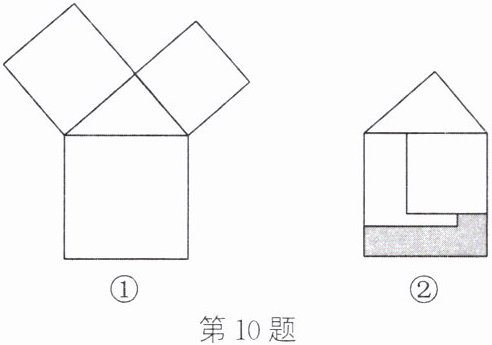
10. 如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两个正方形按如图②所示的方式放置在最大的正方形内.如果知道图中涂色部分的面积,那么一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和

答案： C 解析:设直角三角形的斜边长为c,较长直角边长为b,较短直角边长为a.由勾股定理,得$c^{2}=a^{2}+b^{2}$.涂色部分的面积$=c^{2}-b^{2}-a^{2}+$较小两个正方形重叠部分的面积=较小两个正方形重叠部分的面积.

11. 若3,4,$a$和5,$b$,13是两组勾股数,则$a + b$的值是______.

答案： 17

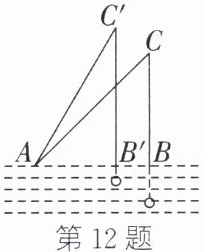
12. 如图,露在水面上的鱼线$BC长为3\mathrm{m}$,钓鱼者把鱼竿$AC提起到AC'$的位置,此时露在水面上的鱼线$B'C'长为4\mathrm{m}$.若$BB'的长为1\mathrm{m}$,则鱼竿$AC$的长为______$\mathrm{m}$.

答案： 5

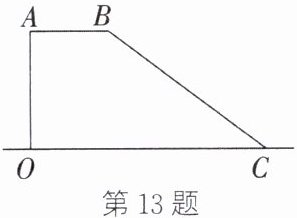
13. 如图,一旗杆从离地面$3\mathrm{m}$、$5\mathrm{m}$两处折成三段,中间一段$AB$恰好与地面平行,旗杆顶部落在离旗杆底部$6\mathrm{m}$处,旗杆折断之前的高度是______$\mathrm{m}$.

答案： 10

14. 一架$25\mathrm{m}$长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端$7\mathrm{m}$.如果梯子的顶端沿墙下滑$4\mathrm{m}$,那么梯脚将水平滑动______$\mathrm{m}$.

答案： 8

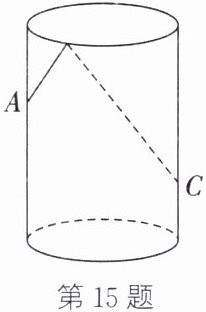
15. 如图,圆柱形玻璃杯的高为$11\mathrm{cm}$,底面周长为$18\mathrm{cm}$,在杯内离杯底$3\mathrm{cm}的点C$处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿$4\mathrm{cm}与蜂蜜相对的点A$处,则蚂蚁到达蜂蜜的最短距离为______$\mathrm{cm}$.

答案： 15 解析:如图所示为玻璃杯侧面展开图的一半,作点A关于EF的对称点$A'$,连接$A'C$,则$A'C$即为最短距离.由题意及对称性,易得$A'E=AE=DF=4\ \text{cm},CD=CF+DF=12\ \text{cm}$.因为底面周长为18 cm,所以$A'D=9\ \text{cm}$.所以在$\text{Rt}\triangle A'DC$中,$A'C^{2}=A'D^{2}+CD^{2}=9^{2}+12^{2}=225(\text{cm}^{2})$.所以$A'C=15\ \text{cm}$,即蚂蚁到达蜂蜜的最短距离是15 cm.

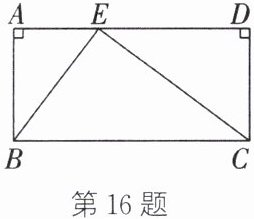
16. (6分)如图,$\angle A= \angle D = 90^{\circ}$,$AB = CD = 12\mathrm{cm}$,$AD = BC = 25\mathrm{cm}$,$E是AD$上一点,且$AE = 9\mathrm{cm}$,连接$BE$,$CE$.判断$\angle BEC$是锐角、钝角还是直角,并说明理由.

答案： $\angle BEC$是直角.理由:因为$AD=BC=25\ \text{cm},AE=9\ \text{cm}$,所以$ED=16\ \text{cm}$.在$\text{Rt}\triangle ABE$中,$BE^{2}=AB^{2}+AE^{2}=12^{2}+9^{2}=225(\text{cm}^{2})$.在$\text{Rt}\triangle CDE$中,$CE^{2}=CD^{2}+ED^{2}=12^{2}+16^{2}=400(\text{cm}^{2})$.又因为$BC^{2}=25^{2}=625(\text{cm}^{2})$,所以$BC^{2}=BE^{2}+CE^{2}$.所以$\triangle BCE$是直角三角形,且$\angle BEC$是直角.