《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

12. 计算$-(x^{3})^{4}÷x^{6}$的结果为____.

答案： $-x^{6}$

13. 如图,对于任意非零整数n按下列程序进行计算：
用代数式表示该程序的运算为____,化简为____.

答案： $(2n^{2}+n)÷ n-n$ $n+1$

14. (乐山中考)已知$a-b= 3,ab= 10$,则$a^{2}+b^{2}= $____.

答案： 29

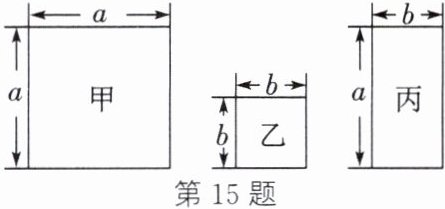
15. 现有甲、乙、丙三种不同的纸片(如图)各若干张. 嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲种纸片1张,再取乙种纸片4张,还需取丙种纸片____张.
答案讲解

答案： 4

16. (8分)(1)先化简,再求值：
$[3(x-y)]^{2}-(36x^{3}y^{2}-16x^{2}y^{3})÷4xy^{2}$,其中$x= -3,y= -\frac {1}{3}$；
(2)用简便方法计算：$2024^{2}-2023×2025$.

答案： （1）原式$=9(x-y)^{2}-(9x^{2}-4xy)=9x^{2}-18xy+9y^{2}-9x^{2}+4xy=9y^{2}-14xy$，当$x=-3$，$y=-\frac{1}{3}$时，原式$=9×(-\frac{1}{3})^{2}-14×(-3)×(-\frac{1}{3})=9×\frac{1}{9}-14×3×\frac{1}{3}=1-14=-13$.（2）原式$=2024^{2}-(2024-1)×(2024+1)=2024^{2}-(2024^{2}-1)=2024^{2}-2024^{2}+1=1$.

17. (10分)一个正方体盲盒的棱长为0.4m.
(1)这个盲盒的体积是多少(用科学记数法表示)？
(2)如果有一个小立方块的棱长为$1×10^{-3}m$,那么需要多少个这样的小立方块才能将盲盒装满？

答案： （1）根据题意可得，$0.4^{3}=6.4×10^{-2}(\text{m}^{3})$，所以这个盲盒的体积是$6.4×10^{-2}\ \text{m}^{3}$.（2）$6.4×10^{-2}÷(1×10^{-3})^{3}=64000000$（个），所以需要64000000个这样的小立方块才能将盲盒装满.

18. ★(12分)(1)下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.
解：$x(x+2y)-(x+1)^{2}+2x$
$=x^{2}+2xy-x^{2}+2x+1+2x$(第一步)
$=2xy+4x+1$(第二步).
① 小颖的化简过程从第____步开始出现错误；
② 对此整式进行化简.
(2)已知$A= 2x+y,B= 2x-y$,求$AB-B^{2}$的值.

答案： （1）① $-$. ② $x(x+2y)-(x+1)^{2}+2x=x^{2}+2xy-x^{2}-2x-1+2x=2xy-1$.（2）因为$A=2x+y$，$B=2x-y$，所以$AB-B^{2}=(2x+y)(2x-y)-(2x-y)^{2}=(4x^{2}-y^{2})-(4x^{2}-4xy+y^{2})=4x^{2}-y^{2}-4x^{2}+4xy-y^{2}=4xy-2y^{2}$.