《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

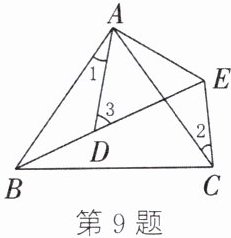
9. 如图,$AB = AC$,$AD = AE$,$\angle BAC = \angle DAE$,$\angle 1 = 25^{\circ}$,$\angle 2 = 30^{\circ}$,则$\angle 3$的度数为( )

A.$55^{\circ}$
B.$50^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$

答案： A 解析：因为∠BAC=∠DAE，所以∠BAC - ∠DAC=∠DAE - ∠DAC. 所以∠1=∠CAE. 在△BAD和△CAE中，AB = AC，∠1 = ∠CAE，AD = AE，所以△BAD≌△CAE. 所以∠ABD = ∠2 = 30°. 因为∠1 = 25°，所以∠ADB = 180° - 30° - 25° = 125°. 所以∠3 = 180° - 125° = 55°.

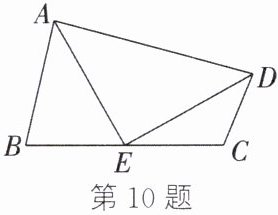
10. 如图,在四边形$ABCD$中,$AB // DC$,$E为BC$的中点,连接$DE$,$AE$,$AE \perp DE$。若$AB = 5$,$CD = 3$,则$AD$的长为( )

A.2
B.5
C.8
D.11

答案：
C 解析：如图，延长DE交AB的延长线于点F. 因为E为BC的中点，所以BE = EC. 因为AB//CD，所以∠F = ∠CDE. 在△BEF和△CED中，∠F = ∠CDE，∠BEF = ∠CED，BE = EC，所以△BEF≌△CED. 所以EF = DE，BF = CD = 3. 所以AF = AB + BF = 8. 因为AE⊥DE，EF = DE，所以AF = AD = 8.

11. 新情境 日常生活 胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这是利用了三角形的______性。

答案： 稳定

12. 已知$\triangle ABC的三个内角度数之比为2:3:4$,则$\triangle ABC$按角分是______三角形。

答案： 锐角

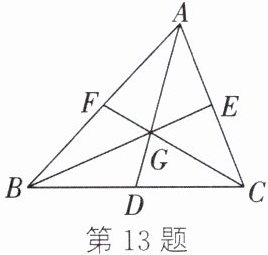
13. 如图,点$G为\triangle ABC$的重心,$D$,$E$,$F分别为BC$,$CA$,$AB$的中点,$AG:GD = BG:GE = CG:GF = 2:1$。若$\triangle AFG$的面积为3,则$\triangle ABC$的面积为______。

答案： 18

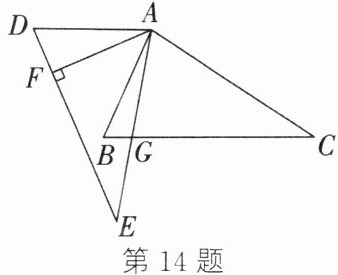
14. 如图,在$\triangle ADE和\triangle ABC$中,$\angle E = \angle C$,$DE = BC$,$EA = CA$,过点$A作AF \perp DE$,垂足为$F$,$AE与BC交于点G$,$\triangle ABG$的面积为8,$AF = 8$,则$BG$的长是______。

答案： 2

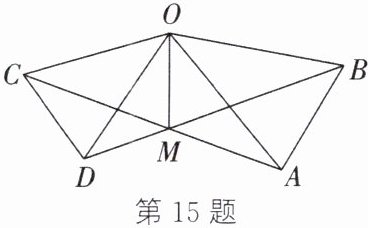
15. 如图,在$\triangle OAB和\triangle OCD$中,$OA = OB$,$OC = OD$,$OA ＞ OC$,$\angle AOB = \angle COD = 40^{\circ}$,连接$AC$,$BD交于点M$,连接$OM$。有下列结论：①$AC = BD$；②$\angle AMB = 40^{\circ}$；③$OM平分\angle BOC$；④$MO平分\angle BMC$。其中,正确的有______(填序号)。

答案：
①②④ 解析：因为∠AOB = ∠COD = 40°，所以∠AOB + ∠AOD = ∠COD + ∠AOD，即∠AOC = ∠BOD. 在△AOC和△BOD中，OA = OB，∠AOC = ∠BOD，OC = OD，所以△AOC≌△BOD. 所以∠OCA = ∠ODB，AC = BD，∠OAC = ∠OBD. 所以①正确. 因为易得∠AMB + ∠OAC = ∠AOB + ∠OBD，所以∠AMB = ∠AOB = 40°. 所以②正确. 如图，过点O作OG⊥MC于点G，作OH⊥MB于点H，则∠OGC = ∠OHD = 90°. 在△OCG和△ODH中，∠OCA = ∠ODB，∠OGC = ∠OHD，OC = OD，所以△OCG≌△ODH. 所以OG = OH. 所以易得MO平分∠BMC. 所以④正确. 因为∠AOB = ∠COD，所以当∠DOM = ∠AOM时，OM才平分∠BOC. 假设∠DOM = ∠AOM. 因为∠AOB = ∠COD，所以易得∠COM = ∠BOM. 因为MO平分∠BMC，所以∠CMO = ∠BMO. 在△COM和△BOM中，∠COM = ∠BOM，OM = OM，∠CMO = ∠BMO，所以△COM≌△BOM. 所以OB = OC. 因为OA = OB，所以OA = OC. 与OA＞OC矛盾，所以③错误. 所以正确的有①②④.

16.(8分)如图,已知线段$a$,$b和\angle \alpha$,按要求用尺规作图(不必写作法,保留作图痕迹)。
(1)求作$\triangle ABC$,使$AB = b$,$BC = a$,$\angle ABC = 2\angle \alpha$；
(2)填空：(1)中作出的三角形______(填“是”或“不是”)唯一的,其作图依据是______。

答案：
（1）如图，△ABC即为所求. （2）是；SAS.