《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

17. (8 分)(1)先化简,再求值：
$ \left[ \left( - \frac { 5 } { 4 } y \right) \cdot ( - 4 y ) + ( x - 2 y ) ^ { 2 } - ( 3 y ) ^ { 2 } \right] \cdot 2 y $,其中 $ x = - 3 $,$ y = \frac { 1 } { 2 } $.
(2)已知 $ 3 x ^ { 2 } + 4 x - 1 = 0 $,求代数式 $ ( 2 x + 1 ) ^ { 2 } - ( x + 1 ) ( x - 1 ) $ 的值.

答案：
(1)原式=(5y²+x²+4y² - 4xy - 9y²)·2y=(x² - 4xy)·2y=2x²y - 8xy². 当 x=-3,y=$\frac{1}{2}$时,原式=2×(-3)²×$\frac{1}{2}$ - 8×(-3)×($\frac{1}{2}$)²=15.
(2)原式=4x²+4x+1 - x²+1=3x²+4x+2. 因为 3x²+4x - 1=0,所以 3x²+4x=1. 所以原式=1+2=3. 所以(2x+1)² - (x+1)(x - 1)的值为 3.

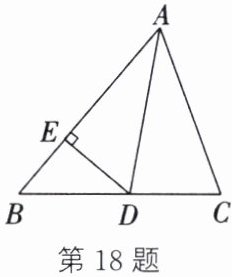
18. (8 分)如图,在 $ \triangle A B C $ 中,$ \angle B = 50 ^ { \circ } $,$ \angle C = 70 ^ { \circ } $,$ A D $ 是 $ \triangle A B C $ 的角平分线,$ D E \perp A B $ 于点 $ E $.
(1)求 $ \angle E D A $ 的度数；
(2)若 $ A B = a $,$ A C = b $,$ D E = c $,求 $ \triangle A B C $ 的面积.

答案：
(1)因为∠B=50°,∠C=70°,所以∠BAC=180° - ∠B - ∠C=60°. 因为 AD 是△ABC 的角平分线,所以∠BAD=$\frac{1}{2}$∠BAC=30°. 因为 DE⊥AB,所以∠DEA=90°. 所以∠EDA=90° - ∠BAD=60°.
(2)过点 D 作 DF⊥AC 于点 F. 因为 AD 是△ABC 的角平分线,DE⊥AB,所以 DF=DE=c. 又因为 AB=a,AC=b,所以 S△ABC=S△ABD+S△ACD=$\frac{1}{2}$AB·DE+$\frac{1}{2}$AC·DF=$\frac{1}{2}$ac+$\frac{1}{2}$bc=$\frac{1}{2}$c(a+b).

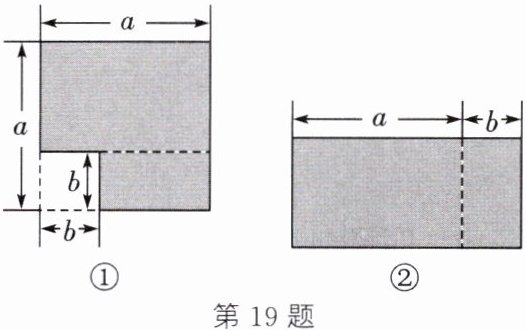
19. (8 分)如图①,从边长为 $ a $ 的大正方形中剪掉一个边长为 $ b $ 的小正方形,将涂色部分按图①中的虚线剪开,拼成如图②所示的长方形.
(1)比较两图涂色部分的面积,可以得到乘法公式：______(用字母 $ a $,$ b $ 表示).
(2)请运用(1)中得到的公式计算下面各题：
① $ ( 2 a + b - c ) ( 2 a - b + c ) $；
② $ 100 ^ { 2 } - 99 ^ { 2 } + 98 ^ { 2 } - 97 ^ { 2 } + … + 4 ^ { 2 } - 3 ^ { 2 } + 2 ^ { 2 } - 1 ^ { 2 } $.

答案：
(1)a² - b²=(a - b)(a+b).
(2)①(2a+b - c)(2a - b+c)=(2a)² - (b - c)²=4a² - b²+2bc - c². ②100² - 99²+98² - 97²+…+4² - 3²+2² - 1²=(100+99)×(100 - 99)+(98+97)×(98 - 97)+…+(2+1)×(2 - 1)=100+99+98+97+…+2+1=$\frac{(100+1)×100}{2}$=5050.