《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

9. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 5$,$BC= 12$,$CO\perp AB于点O$。求：
(1)$AB$的长；
(2)$AO$的长。

答案： （1）因为在$\triangle ABC$中，$\angle ACB=90^{\circ}$，所以$AC^{2}+BC^{2}=AB^{2}$.因为$AC=5$，$BC=12$，所以$AB^{2}=5^{2}+12^{2}=169$.所以$AB=13$.（2）因为$\angle ACB=90^{\circ}$，$CO\perp AB$，所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CO$，即$AC\cdot BC=AB\cdot CO$.所以$5×12=13CO$.所以$CO=\frac{60}{13}$.因为在$\text{Rt}\triangle AOC$中，$AO^{2}+CO^{2}=AC^{2}$，所以$AO^{2}=AC^{2}-CO^{2}=5^{2}-\left(\frac{60}{13}\right)^{2}=\frac{625}{169}$.所以$AO=\frac{25}{13}$.

10. 如图,在$Rt\triangle ABC$中,$\angle A= 90^{\circ}$,$AB= 8$,$AC= 15$,以点$B$为圆心,适当长为半径画弧,分别交$BA$,$BC于点M$,$N$,再分别以点$M$,$N$为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧交于点$E$,作射线$BE$,交$AC于点D$,求$AD$的长。

答案： 因为在$\text{Rt}\triangle ABC$中，$\angle A=90^{\circ}$，所以$AB^{2}+AC^{2}=BC^{2}$.因为$AB=8$，$AC=15$，所以易得$BC=17$.如图，过点$D$作$DH\perp BC$于点$H$，则$\angle BHD=\angle A=90^{\circ}$.根据题意，易得$BD$平分$\angle ABC$，所以$\angle ABD=\angle HBD$.又因为$BD=BD$，所以$\triangle ABD\cong\triangle HBD$.所以$HB=AB=8$，$AD=HD$.所以$CH=BC - HB=9$.因为在$\text{Rt}\triangle DHC$中，$CH^{2}+DH^{2}=CD^{2}$，所以$9^{2}+AD^{2}=(15 - AD)^{2}$.所以$AD=\frac{24}{5}$.

11. 如图所示为由两个直角三角形和三个正方形组成的图形,其中涂色部分的面积是( )

A.16
B.25
C.144
D.169

答案： B

12. 如图,在离水面高度为$8m$的岸上,有人用绳子拉船靠岸,开始时绳子$BC的长为17m$,几分钟后船到达点$D$的位置,此时绳子$CD的长为10m$,则船向岸边移动了______$m$。

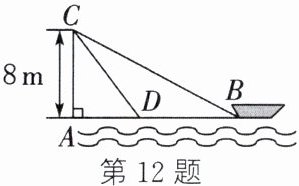
答案： 9

13. 如图,某工厂大门的上面是半圆,下面是长方形。一辆装满货物的卡车,高$2.5m$,宽$1.6m$。这辆卡车能否通过厂门？请说明理由。

答案： 这辆卡车能通过厂门.理由：如图，$MN$为卡车的宽度，分别过点$M$，$N$作$AB$的垂线交半圆于点$C$，$D$，连接$CD$，过点$O$作$OE\perp CD$，垂足为$E$，连接$OC$，则易得$CD=MN=1.6\ \text{m}$，$AB=2\ \text{m}$，所以易得$CE=DE=0.8\ \text{m}$，$OC=OA=\frac{1}{2}AB=1\ \text{m}$.在$\text{Rt}\triangle OCE$中，$OE^{2}=OC^{2}-CE^{2}=1^{2}-0.8^{2}=0.36\ (\text{m}^{2})$，所以$OE=0.6\ \text{m}$.所以$CM=2.3+0.6=2.9(\text{m})$.因为$2.9\ \text{m}＞2.5\ \text{m}$，所以这辆卡车能通过厂门.