《2025年通城学典暑期升级训练七年级数学北师大版延边大学出版社》

6. 如图,第1个图形由1个正六边形、6个正方形和6个等边三角形组成；第2个图形由2个正六边形、11个正方形和10个等边三角形组成；第3个图形由3个正六边形、16个正方形和14个等边三角形组成……按照此规律,第n个图形中,正方形和等边三角形一共有______个(用含n的代数式表示)。

答案： (9n+3)

7. 如图所示为用图形“$◯$”和“$\odot$”按一定规律摆成的“小屋子”。按照此规律继续摆下去,第n个“小屋子”中图形“$◯$”的个数为______,“$\odot$”的个数为______。

答案： $\frac{n(n+1)}{2}$ 2n+2 解析:由所给图形可知,第1个“小屋子”中图形“○”的个数为1=1,“◎”的个数为4=1×2+2;第2个“小屋子”中图形“○”的个数为3=1+2,“◎”的个数为6=2×2+2;第3个“小屋子”中图形“○”的个数为6=1+2+3,“◎”的个数为8=3×2+2;第4个“小屋子”中图形“○”的个数为10=1+2+3+4,“◎”的个数为10=4×2+2;…,所以第n个“小屋子”中图形“○”的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$,“◎”的个数为2n+2.

8. 观察下列数据：$\frac{1}{2},-\frac{2}{5},\frac{3}{10},-\frac{4}{17},\frac{5}{26},…$。第12个数是( )

A.$\frac{12}{143}$
B.$-\frac{12}{143}$
C.$\frac{12}{145}$
D.$-\frac{12}{145}$

答案： D

9. (扬州中考)1202年数学家斐波那契在《计算之书》中记载了一列数：$1,1,2,3,5,…$。这一列数满足：从第三个数开始,每一个数都等于它的前面两个数之和。在这一列数的前2024个数中,奇数的个数为( )

A.676
B.674
C.1348
D.1350

答案： D

10. (常德中考)如图,横排为行,竖排为列,按其中的规律,分数$\frac{20}{2023}$若排在第a行第b列,则$a - b$的值为( )

A.2003
B.2004
C.2022
D.2023

答案： C 解析:观察图中的规律发现,分数的分子是几,则必在第几列;只有第一列的分数,分母与其所在行数一致,故$\frac{20}{2023}$在第20列,即b=20;向前递推到第1列时,分数为$\frac{20-19}{2023+19}=\frac{1}{2042}$,故分数$\frac{20}{2023}$与分数$\frac{1}{2042}$在同一行,即在第2042行.则a=2042.所以a-b=2042-20=2022.

11. 归纳思想(江西中考)观察$a,a^{2},a^{3},a^{4},…$,根据这些式子的变化规律,可得第100个式子为______。

答案： $a^{100}$

12. 如图所示为一个运算程序的示意图,若开始输入x的值为625,则第2023次输出的结果为______。

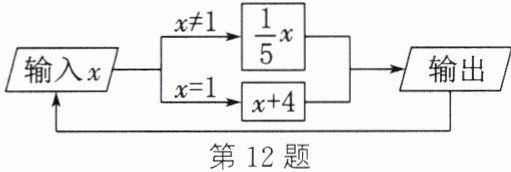
答案： 5 解析:当x=625时,$\frac{1}{5}x=125$;当x=125时,$\frac{1}{5}x=25$;当x=25时,$\frac{1}{5}x=5$;当x=5时,$\frac{1}{5}x=1$;当x=1时,x+4=5;当x=5时,$\frac{1}{5}x=1$;…,所以输出的结果从第3次开始按5,1为一组循环.因为(2023-2)÷2=1010(组)……1(次),所以第2023次输出的结果和第3次相同,为5.

13. (恩施中考)观察下面两行数,探究第②行数与第①行数的关系：
$-2,4,-8,16,-32,64,…$。①
$0,7,-4,21,-26,71,…$。②
根据你的发现,完成填空：第①行数的第10个数为______；取每行数的第2023个数,则这两个数的和为______。

答案： 1024 $-2^{2024}+2024$

14. 观察等式：$2 + 2^{2} = 2^{3} - 2,2 + 2^{2} + 2^{3} = 2^{4} - 2,2 + 2^{2} + 2^{3} + 2^{4} = 2^{5} - 2,…$。已知按一定规律排列的一组数：$2^{100},2^{101},2^{102},…,2^{199}$。若$2^{100} = m$,则这组数的和是______(用含m的代数式表示)。

答案： $m^2-m$ 解析:由题意,得$2^{100}+2^{101}+2^{102}+\dots +2^{199}=(2^2+2^3+2^4+\dots +2^{199})-(2+2^2+2^3+\dots +2^{99})=(2^{200}-2)-(2^{100}-2)=(2^{100})^2-2^{100}=m^2-m$.

15. 设$\overline{a5}$是一个两位数,其中$a(1\leqslant a\leqslant9)$是十位上的数字。例如,当$a = 4$时,$\overline{a5}$表示的两位数是45。
(1)尝试：
① 当$a = 1$时,$15^{2} = 225 = 1×2×100 + 25$；
② 当$a = 2$时,$25^{2} = 625 = 2×3×100 + 25$；
③ 当$a = 3$时,$35^{2} = 1225 = $______。
(2)归纳：$\overline{a5}^{2}与100a(a + 1) + 25$之间有怎样的大小关系？请说明理由。

答案：
(1) ③ 3×4×100+25.
(2) $\overline{a5}^2=100a(a+1)+25$.理由:$\overline{a5}^2=(10a+5)(10a+5)=100a^2+100a+25=100a(a+1)+25$.