《2025年暑假作业江西教育出版社七年级合订本北师大版》

1. 如图,书架两侧摆放了若干本相同的书籍,左右两摞书中竖直放入一个等腰直角三角尺,其直角顶点C在书架底部DE上。当顶点A落在右侧书籍的上方边沿时,顶点B恰好落在左侧书籍的上方边沿。若每本书长20cm,厚度为2cm,则两摞书之间的距离DE为()

A. 24cm
B. 23cm
C. 22cm
D. 21cm

答案： C

2. 如图,为了测量容器底部内径CD,小明将两根细木条的中点固定在一起,通过测量A,B两点之间的距离,得到CD的长度。其依据的数学原理是()

A. 三边分别相等的两个三角形全等
B. 两边及其夹角分别相等的两个三角形全等
C. 两角及其夹边分别相等的两个三角形全等
D. 两点之间,线段最短

答案： B

3. 如图,要测量水池的宽AB,可以过点A作AC⊥AB,再由点C观测,在BA的延长线上找一点B',使∠ACB'= ∠ACB,这时测得AB'的长就是AB的长。这个测量方法用到了判定三角形全等的依据中的______。

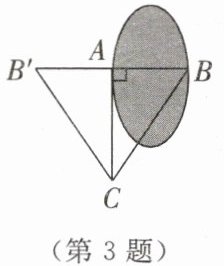
答案： $ASA$

4. (1)如图①,折叠凳具有一定的稳定性,这种设计所运用的数学原理是什么?
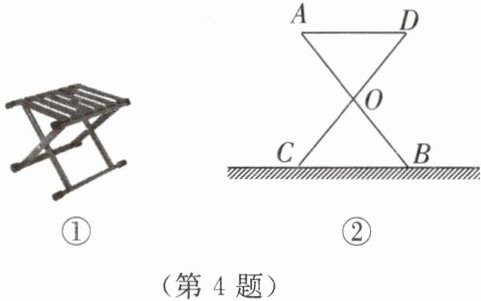
(2)折叠凳撑开后的侧面示意图如图②所示,其中凳腿AB和CD的长度相等,O是它们的中点。若折叠凳的宽AD为38cm,则BC的长度是多少?(木条等材料的宽度忽略不计)

答案： 【解析】：
(1) 三角形具有稳定性，折叠凳的设计中，通过凳腿等结构形成了三角形，所以运用的数学原理是三角形的稳定性。
(2) 因为$O$是$AB$和$CD$的中点，所以$AO = BO$，$DO = CO$。
在$\triangle AOD$和$\triangle BOC$中：
$\begin{cases}AO = BO\\\angle AOD=\angle BOC（对顶角相等）\\DO = CO\end{cases}$
根据“边角边”（$SAS$）定理可得$\triangle AOD\cong\triangle BOC$。
全等三角形的对应边相等，因为$AD = 38cm$，所以$BC = AD = 38cm$。
【答案】：
(1) 三角形的稳定性。
(2)$38cm$。