《2025年全品学练考九年级数学上册苏科版江苏专版》

总结

反思
举例说明如何选用解一元二次方程的方法.

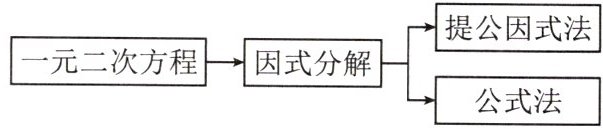
答案： 1. 首先看方程是否能直接因式分解：
例如方程$x^{2}-5x + 6 = 0$，
解：对$x^{2}-5x + 6$进行因式分解，根据$x^{2}+(a + b)x+ab=(x + a)(x + b)$，这里$a=-2$，$b=-3$，则$x^{2}-5x + 6=(x - 2)(x - 3)$，
原方程化为$(x - 2)(x - 3)=0$，
根据“若$ab = 0$，则$a = 0$或$b = 0$”，可得$x-2 = 0$或$x - 3 = 0$，
解得$x_{1}=2$，$x_{2}=3$。
2. 若不能直接因式分解，再看是否能配方法：
例如方程$x^{2}+6x-7 = 0$，
解：配方，$x^{2}+6x-7=(x^{2}+6x+9)-9 - 7$，
根据完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$（这里$a = x$，$b = 3$），则$x^{2}+6x+9=(x + 3)^{2}$，
原方程化为$(x + 3)^{2}-16 = 0$，即$(x + 3)^{2}=16$，
开平方得$x + 3=\pm4$，
当$x + 3 = 4$时，$x=1$；当$x + 3=-4$时，$x=-7$。
3. 若配方法也较复杂，就用公式法：
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
例如方程$2x^{2}-3x - 1 = 0$，其中$a = 2$，$b=-3$，$c=-1$，
先计算判别式$\Delta=b^{2}-4ac=(-3)^{2}-4×2×(-1)=9 + 8 = 17$，
再代入求根公式$x=\frac{-(-3)\pm\sqrt{17}}{2×2}=\frac{3\pm\sqrt{17}}{4}$，
所以$x_{1}=\frac{3+\sqrt{17}}{4}$，$x_{2}=\frac{3-\sqrt{17}}{4}$。
一般来说，能直接因式分解的优先用因式分解法；不能直接因式分解但一次项系数是偶数等情况可尝试配方法；对于一般形式的一元二次方程都可以用公式法。