《2025年全品学练考九年级数学上册苏科版江苏专版》

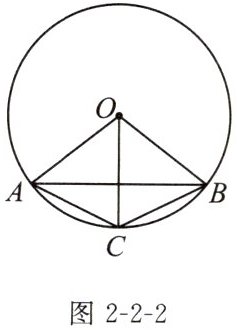
例1 (教材典题)如图2-2-2,$AB$,$AC$,$BC是\odot O$的弦,$∠AOC= ∠BOC$.$∠ABC与∠BAC$相等吗？为什么？

答案： 解：$\angle ABC$与$\angle BAC$相等。
理由：在$\odot O$中，
$\because \angle AOC = \angle BOC$，
$\therefore AC = BC$（在同圆中，相等的圆心角所对的弦相等）。$\therefore \angle ABC = \angle BAC$。

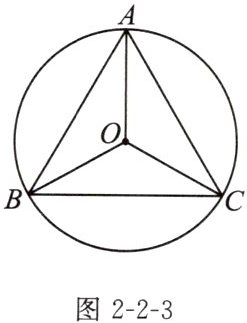
例2 如图2-2-3,在$\odot O$中,$\overset{\frown}{AB}= \overset{\frown}{AC}$,$∠ACB= 60^{\circ}$.
求证：$∠AOB= ∠BOC= ∠AOC$.

答案： 证明：$\because \overset{\frown}{AB} = \overset{\frown}{AC}$，$\therefore AB = AC$，
$\therefore \triangle ABC$是等腰三角形。
$\because \angle ACB = 60^{\circ}$，
$\therefore \triangle ABC$是等边三角形，
$\therefore AB = BC = CA$，
$\therefore \angle AOB = \angle BOC = \angle AOC$。