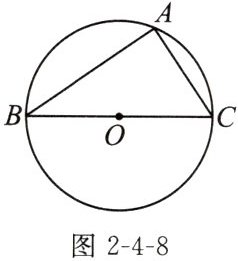
1. 如图2-4-8,BC是$\odot O$的直径,A是$\odot O$上任意一点,请你确定$∠BAC$的度数.

答案:
解:$\angle BAC = 90^{\circ}$。
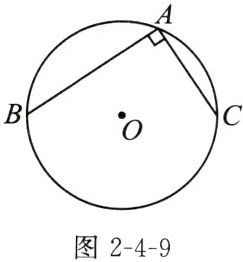
2. 如图2-4-9,在$\odot O$中,圆周角$∠BAC= 90^{\circ }$,弦BC经过圆心O吗?

答案:
解:连接 $BO$,$CO$。
∵ $\angle BAC$ 所对的弧是 $\overset{\frown}{BC}$,$\angle BAC = 90^{\circ}$,
∴ $\angle BOC$ 的度数为 $180^{\circ}$。
∴ 点 $B$,$O$,$C$ 在一条直线上。
∴ 弦 $BC$ 经过圆心 $O$。
∵ $\angle BAC$ 所对的弧是 $\overset{\frown}{BC}$,$\angle BAC = 90^{\circ}$,
∴ $\angle BOC$ 的度数为 $180^{\circ}$。
∴ 点 $B$,$O$,$C$ 在一条直线上。
∴ 弦 $BC$ 经过圆心 $O$。
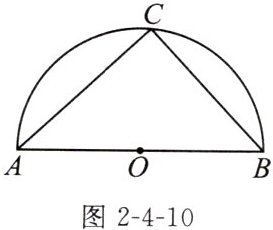
例1 如图2-4-10,已知AB是半圆O的直径,C是$\widehat {AB}$的中点,且$AC= 3$,求直径AB的长.

答案:
$3\sqrt{2}$
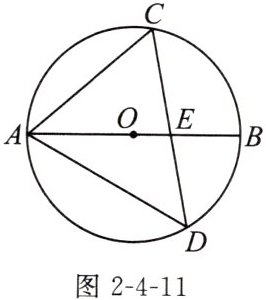
例2(教材典题)如图2-4-11,AB是$\odot O$的直径,弦CD交AB于点E,$∠ACD= 60^{\circ },∠ADC= 50^{\circ }$.求$∠CEB$的度数.

答案:
$100^{\circ}$
查看更多完整答案,请扫码查看


