《2025年全品学练考九年级数学上册苏科版江苏专版》

如图2-5-3,设⊙O的半径为r,圆心O到直线l的距离为d.

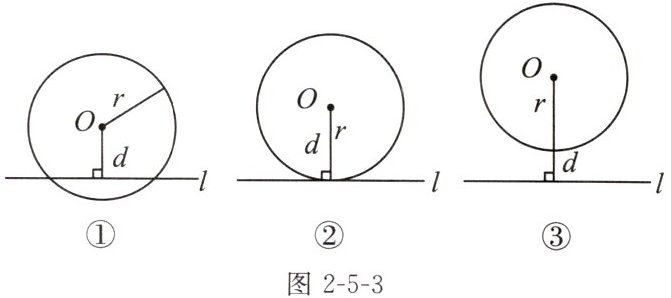
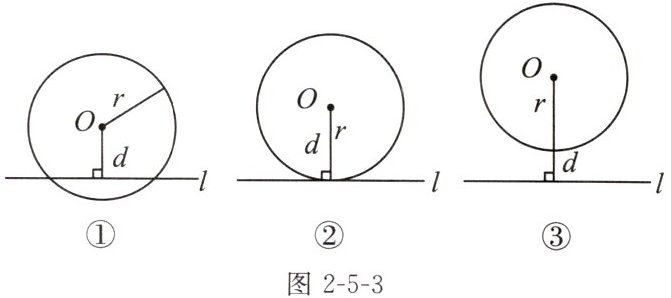
图①中,直线l与⊙O有两个公共点,直线l与⊙O相交(位置关系),此时,d＜r(填“＞”“=”或“＜”)；
图②中,直线l与⊙O有一个公共点,直线l与⊙O相切(位置关系),此时,d=r(填“＞”“=”或“＜”)；
图③中,直线l与⊙O没有公共点,直线l与⊙O相离(位置关系),此时,d＞r(填“＞”“=”或“＜”).

答案： 两 相交 ＜ 一 相切 = 没有 相离 ＞

例1 (教材典题)已知∠BAC= 45°,点O在AC上,且AO= 4,以点O为圆心,r为半径画圆.根据下列r的值,判断AB所在直线与⊙O的位置关系：
(1)r= 2；(2)r= 2√2；(3)r= 3.

答案：
解:如图①②③，过点O作OD⊥AB，垂足为D。
在Rt△AOD中，
∵∠A = 45°，
∴∠AOD = ∠A，OD = AD。
又
∵OD² + AD² = AO²，AO = 4，
∴2OD² = 16，OD = 2√2，
即圆心O到AB所在直线的距离d = 2√2。

(1)如图①，当r = 2时，d ＞ r，AB所在直线与⊙O相离。
(2)如图②，当r = 2√2时，d = r，AB所在直线与⊙O相切。
(3)如图③，当r = 3时，d ＜ r，AB所在直线与⊙O相交。