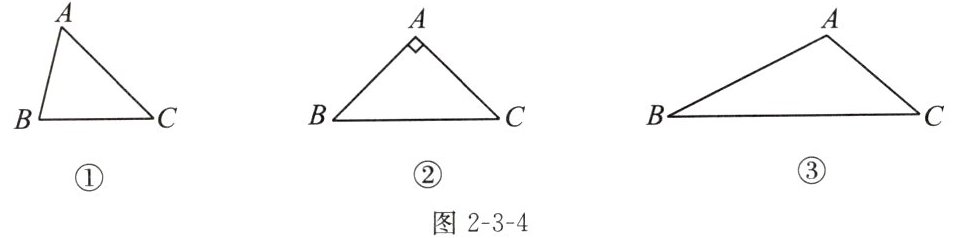
例1 已知$\triangle ABC$,用直尺和圆规作$\triangle ABC$的外接圆(保留作图痕迹,不写作法).
(1)如图2-3-4①,$\triangle ABC$是锐角三角形;
(2)如图②,$\triangle ABC$是直角三角形,且$∠A= 90^{\circ }$;
(3)如图③,$\triangle ABC$是钝角三角形,且$∠A$是钝角.
(1)如图2-3-4①,$\triangle ABC$是锐角三角形;
(2)如图②,$\triangle ABC$是直角三角形,且$∠A= 90^{\circ }$;
(3)如图③,$\triangle ABC$是钝角三角形,且$∠A$是钝角.

答案:
例1 解:如图.

例1 解:如图.

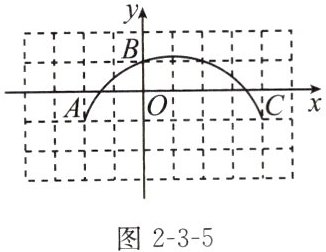
例2 如图2-3-5,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角坐标系.
(1)过A,B,C三点的圆$\odot M$的圆心M的坐标为____
(2)请通过计算判断点$D(-3,-2)与\odot M$的位置关系.
(1)过A,B,C三点的圆$\odot M$的圆心M的坐标为____
(-1,0)
;(2)请通过计算判断点$D(-3,-2)与\odot M$的位置关系.
点D在$\odot M$外

答案:
1. (1)
根据圆的性质:圆的垂直平分线的交点是圆心。
作$AB$和$BC$的垂直平分线,交点$M$的坐标为$(-1,0)$。
2. (2)
解:
已知$M(-1,0)$,$D(-3,-2)$,根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$(其中$(x_1,y_1)$,$(x_2,y_2)$为两点坐标),先求$\odot M$的半径$r$。
取$A(-3,0)$,则$r=\vert MA\vert=\sqrt{(-1 + 3)^2+(0 - 0)^2}=2$。
再求$MD$的距离,$x_1=-1,y_1 = 0,x_2=-3,y_2=-2$,$MD=\sqrt{(-1+3)^2+(0 + 2)^2}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
比较$MD$与$r$的大小,因为$2\sqrt{2}\approx2×1.414 = 2.828\gt2$。
所以(1)$(-1,0)$;(2)点$D$在$\odot M$外。
根据圆的性质:圆的垂直平分线的交点是圆心。
作$AB$和$BC$的垂直平分线,交点$M$的坐标为$(-1,0)$。
2. (2)
解:
已知$M(-1,0)$,$D(-3,-2)$,根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$(其中$(x_1,y_1)$,$(x_2,y_2)$为两点坐标),先求$\odot M$的半径$r$。
取$A(-3,0)$,则$r=\vert MA\vert=\sqrt{(-1 + 3)^2+(0 - 0)^2}=2$。
再求$MD$的距离,$x_1=-1,y_1 = 0,x_2=-3,y_2=-2$,$MD=\sqrt{(-1+3)^2+(0 + 2)^2}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
比较$MD$与$r$的大小,因为$2\sqrt{2}\approx2×1.414 = 2.828\gt2$。
所以(1)$(-1,0)$;(2)点$D$在$\odot M$外。
如图2-3-6,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中点E在$\triangle ABC$的外部,下列叙述不正确的是 (
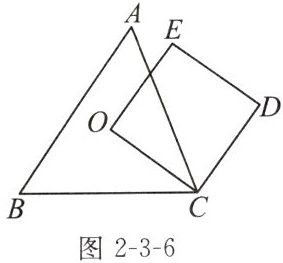
A. O是$\triangle AEB$的外心,O不是$\triangle AED$的外心
B. O是$\triangle BEC$的外心,O不是$\triangle BCD$的外心
C. O是$\triangle AEC$的外心,O不是$\triangle CDE$的外心
D. O是$\triangle ADB$的外心,O不是$\triangle ADC$的外心
D
)
A. O是$\triangle AEB$的外心,O不是$\triangle AED$的外心
B. O是$\triangle BEC$的外心,O不是$\triangle BCD$的外心
C. O是$\triangle AEC$的外心,O不是$\triangle CDE$的外心
D. O是$\triangle ADB$的外心,O不是$\triangle ADC$的外心
答案:
[课堂总结与反思]
|反思|
D
|反思|
D
查看更多完整答案,请扫码查看


