《2025年全品学练考九年级数学上册苏科版江苏专版》

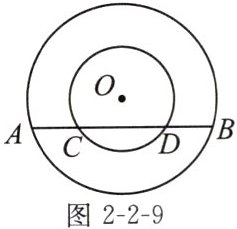
例1(教材典题)如图2-2-9,在以点$O$为圆心的两个同心圆中,大圆的弦$AB交小圆于点C$,$D$。$AC与BD$相等吗？为什么？

答案： 例1　$AC$与$BD$相等。理由略

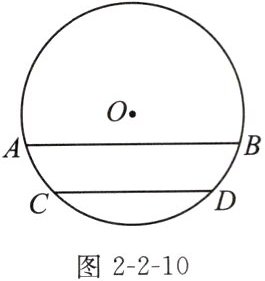
拓展 如图2-2-10,$AB$,$CD是\odot O$的两条弦,$AB// CD$,$\overset{\frown}{AC}与\overset{\frown}{BD}$相等吗？为什么？

答案：
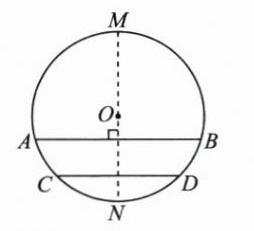
拓展　解：$\overset{\frown}{AC}=\overset{\frown}{BD}$。理由如下：如图，作垂直于弦$AB$的直径$MN$，则由$AB// CD$，可得$MN\perp CD$。

$\because MN\perp AB$，$MN\perp CD$，
$\therefore \overset{\frown}{AM}=\overset{\frown}{BM}$，$\overset{\frown}{CM}=\overset{\frown}{DM}$。
$\therefore \overset{\frown}{CM}-\overset{\frown}{AM}=\overset{\frown}{DM}-\overset{\frown}{BM}$。
即$\overset{\frown}{AC}=\overset{\frown}{BD}$。

例2 $\odot O的半径为13\mathrm{cm}$,$AB$,$CD是\odot O$的两条弦,$AB// CD$,$AB= 24\mathrm{cm}$,$CD= 10\mathrm{cm}$,求$AB与CD$之间的距离。

答案：
例2　解：连接$OA$，$OC$，过点$O$作$OF\perp CD$，垂足为$F$，$OF$（或其反向延长线）与$AB$交于点$E$。
$\because AB// CD$，$\therefore OE\perp AB$。
$\because AB=24\mathrm{cm}$，$CD=10\mathrm{cm}$，
$\therefore AE=12\mathrm{cm}$，$CF=5\mathrm{cm}$。
$\because OA=OC=13\mathrm{cm}$，
$\therefore OE=5\mathrm{cm}$，$OF=12\mathrm{cm}$。
当弦$AB$，$CD$在圆心$O$同侧时，如图①。
$EF=OF - OE=12 - 5=7(\mathrm{cm})$。

当弦$AB$，$CD$在圆心$O$异侧时，如图②。
$EF=OF + OE=12 + 5=17(\mathrm{cm})$。
综上，$AB$与$CD$之间的距离为$7\mathrm{cm}$或$17\mathrm{cm}$。

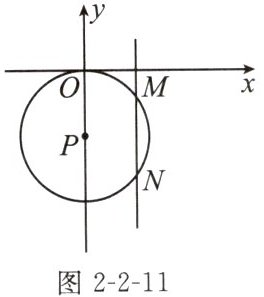
如图2-2-11,点$P在y$轴上,过坐标原点的$\odot P与平行于y轴的直线交于M$,$N$两点。若点$M的坐标是(2,-1)$,则点$N$的坐标为(2,-4)。

答案： |反思|
$(2,-4)$