观察思考
如图2-5-6,直线l与$\odot O$相切于点A,则半径OA垂直于直线l.为什么?
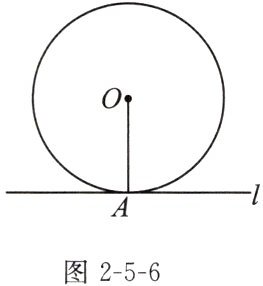
如图2-5-6,直线l与$\odot O$相切于点A,则半径OA垂直于直线l.为什么?

答案:
解:假设 OA 与直线 l 不垂直,过点 O 作$OM⊥l$,垂足为 M,
则$OM<OA$,即圆心 O 到直线 l 的距离小于⊙O 的半径,因此,直线 l 与⊙O 相交,
这与已知条件“直线 l 与⊙O 相切”相矛盾,
∴OA 垂直于直线 l.
则$OM<OA$,即圆心 O 到直线 l 的距离小于⊙O 的半径,因此,直线 l 与⊙O 相交,
这与已知条件“直线 l 与⊙O 相切”相矛盾,
∴OA 垂直于直线 l.
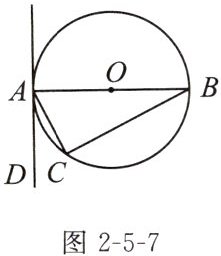
例1(教材典题)如图2-5-7,$\triangle ABC是\odot O$的内接三角形,AB是$\odot O$的直径,$\angle CAD= \angle ABC$.判断直线AD与$\odot O$的位置关系,并说明理由.

答案:
直线 AD 与⊙O 相切.理由略
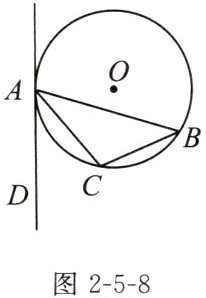
变式 如图2-5-8,$\triangle ABC是\odot O$的内接三角形,$\angle CAD= \angle ABC$.判断直线AD与$\odot O$的位置关系,并说明理由.

答案:
直线 AD 与⊙O 相切.理由略
查看更多完整答案,请扫码查看


