《2025年全品学练考九年级数学上册苏科版江苏专版》

例2 不解方程,判断下列方程的根的情况.
(1)$3x^{2}+4x-3= 0$; (2)$4x^{2}= 12x-9$; (3)$7y= 5(y^{2}+1)$.

答案： 解:
(1)$a=3,b=4,c=-3$, $\therefore b^{2}-4ac=4^{2}-4×3×(-3)=52＞0$. $\therefore$原方程有两个不相等的实数根.  
(2)方程化为$4x^{2}-12x+9=0$. $\because a=4,b=-12,c=9$, $\therefore b^{2}-4ac=(-12)^{2}-4×4×9=0$. $\therefore$原方程有两个相等的实数根.
(3)方程化为$5y^{2}-7y+5=0$. $\because a=5,b=-7,c=5$, $\therefore b^{2}-4ac=(-7)^{2}-4×5×5=-51＜0$. $\therefore$原方程没有实数根.

拓展 已知关于$x的方程x^{2}+2x-a+1= 0$没有实数根,试判断关于$x的方程x^{2}+ax+a= 0$的根的情况.

答案： 解:$\because$关于$x$的方程$x^{2}+2x-a+1=0$没有实数根, $\therefore 2^{2}-4(-a+1)＜0$, 解得$a＜0$. 方程$x^{2}+ax+a=0$的根的判别式是$a^{2}-4a=a(a-4)$. $\because a＜0,\therefore a-4＜0$, $\therefore a(a-4)＞0$, $\therefore$关于$x$的方程$x^{2}+ax+a=0$有两个不相等的实数根. 

课堂总结与反思

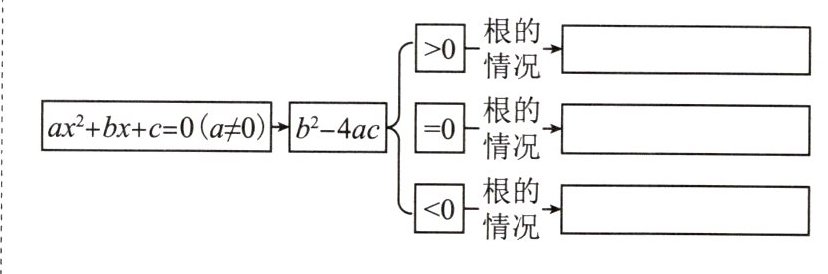
答案： 本题可根据一元二次方程根的判别式$\Delta = b^{2}-4ac$与根的关系来填空。
- **当$\boldsymbol{b^{2}-4ac\gt0}$时：
根据一元二次方程$ax^{2}+bx + c = 0(a\neq0)$的求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，当$b^{2}-4ac\gt0$时，$\sqrt{b^{2}-4ac}$有意义，此时方程有两个不相等的实数根。
- **当$\boldsymbol{b^{2}-4ac = 0}$时：
同样根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，当$b^{2}-4ac = 0$时，$\sqrt{b^{2}-4ac}=0$，则$x=\frac{-b}{2a}$，此时方程有两个相等的实数根。
- **当$\boldsymbol{b^{2}-4ac\lt0}$时：
因为在实数范围内，负数没有平方根，所以当$b^{2}-4ac\lt0$时，$\sqrt{b^{2}-4ac}$无意义，此时方程没有实数根。
综上，答案依次为：有两个不相等的实数根；有两个相等的实数根；没有实数根。

试说出一元二次方程的根的情况与系数的关系.

答案： 解：对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其判别式$\Delta=b^{2}-4ac$。
当$\Delta\gt0$时，方程有两个不相等的实数根；
当$\Delta = 0$时，方程有两个相等的实数根；
当$\Delta\lt0$时，方程没有实数根。