《2025年全品学练考九年级数学上册苏科版江苏专版》

例2 如图2-4-18,$\odot O是\triangle ABC$的外接圆,$∠A= 62^{\circ}$,E是BC的中点,连接OE并延长交$\odot O$于点D,连接BD,求$∠D$的度数。

答案： 59°

求证：圆内接四边形的对角互补。
已知：如图2-4-19①,四边形ABCD内接于$\odot O$。
求证：$∠BAD+∠BCD= 180^{\circ}$。
请根据图②中的辅助线,完成证明过程。

答案： 证明：
∵AE为⊙O的直径，
∴∠ADE=∠ABE=90°，
∴∠DAE+∠DEA=90°，∠BAE+∠BEA=90°，
∴∠DAE+∠DEA+∠BAE+∠BEA=180°。
即∠DAB+∠DEB=180°。
∵$\overset{\frown}{BD}=\overset{\frown}{BD}$，
∴∠DCB=∠DEB，
∴∠BAD+∠BCD=180°。

1. 观察三幅太阳升起的照片,地平线与太阳经历了哪些位置关系？通过这个自然现象,你猜想直线和圆的位置关系有哪几种？

答案： 解:有3种位置关系，分别是太阳和地平线有2个公共点，太阳和地平线有1个公共点，太阳和地平线没有公共点。
猜想:有3种位置关系，分别是直线和圆有2个公共点，直线和圆有1个公共点，直线和圆没有公共点。

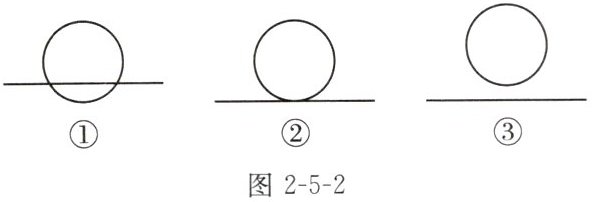
2. 在纸上画一个圆,按图2-5-2①②③的顺序移动直尺.观察一下,直尺上边缘所在直线在移动的过程中与圆的位置关系发生了怎样的变化？

答案： 解:直尺上边缘所在直线在移动过程中先与圆有2个公共点，然后与圆有1个公共点，最后与圆没有公共点。