《2025年全品学练考九年级数学上册苏科版江苏专版》

例1 下列关于$x$的方程中,一定是一元二次方程的为 (D)
A.$x^{2}-2= (x+3)^{2}$
B.$ax^{2}+bx+c= 0$
C.$x^{2}+\frac {3}{x}-5= 0$
D.$x^{2}-1= 0$

答案： D

例2 将下列方程化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项。
(1)$5x^{2}-1= 4x$；
(2)$4x^{2}= 81$；
(3)$(x-2)(3-2x)= 0$。

答案： 解: 答案不唯一.
(1) 整理, 得$5x^{2}-4x - 1=0$.
二次项系数是 5, 一次项系数是 -4, 常数项是 -1.
(2) 整理, 得$4x^{2}-81=0$.
二次项系数是 4, 一次项系数是 0, 常数项是 -81.
(3) 整理, 得$-2x^{2}+7x - 6=0$.
二次项系数是 -2, 一次项系数是 7, 常数项是 -6.

例3 关于$x的方程(m+1)x^{|m-1|}+mx-1= 0$是一元二次方程,则$m$的值为3。

答案： 3

变式1 已知关于$x的方程(m+1)x^{m^{2}+1}+(m-2)x-1= 0$。
(1)当$m$取何值时,它是一元二次方程？
(2)当$m$取何值时,它是一元一次方程？

答案：
(1)1
(2)-1 或 0

变式2 关于$x的一元二次方程(m-3)x^{2}+m^{2}x= 9x+5$化为一般形式后不含一次项,则$m$的值为-3。

答案： -3

课堂总结与反思

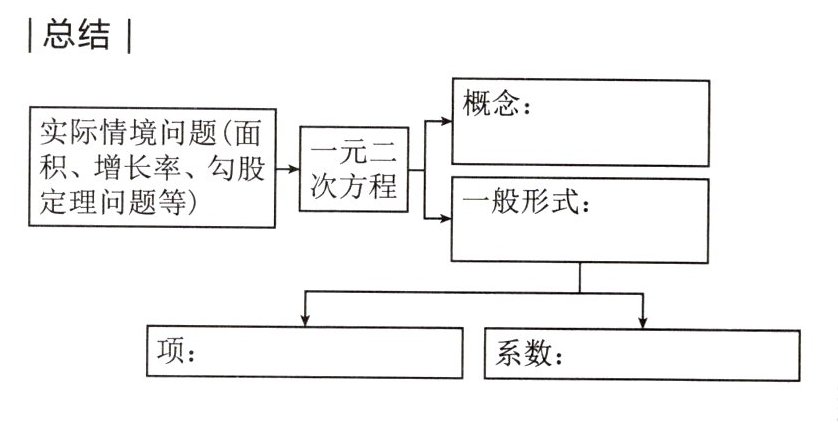
答案： 概念：只含有一个未知数（一元），并且未知数的最高次数是$2$（二次）的整式方程。
一般形式：$ax^{2}+bx + c = 0$（$a\neq0$）。
项：二次项$ax^{2}$，一次项$bx$，常数项$c$。
系数：二次项系数$a$，一次项系数$b$。

用一元二次方程描述实际问题中的数量关系的关键是什么？

答案： 解: 关键是寻找实际问题中的等量关系.