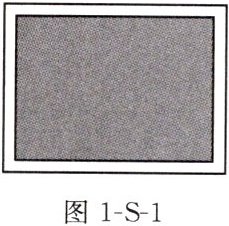
活动一:如图 1-S-1,在一块长是 32 m、宽是 24 m 的矩形绿地内,要围出一个矩形花圃,使花圃面积是矩形面积的一半,四周的绿地等宽.你能计算出绿地的宽吗?

答案:
4m
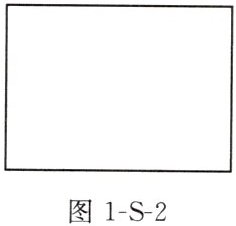
活动二:如图 1-S-2,在一块长是 32 m、宽是 24 m 的矩形绿地内,开辟出横竖两条等宽的小路(两条小路与矩形的边平行),然后在剩余的绿地上开辟花圃,使花圃的面积等于矩形面积的一半,请尝试画出设计草图,并计算小路的宽.

答案:
解:画出图形如图(图形不唯一).
设小路的宽为x m.
根据题意,得$(32-x)(24-x)=\frac {1}{2}×32×24$,
即$x^{2}-56x+384=0$,
解得$x_{1}=48,x_{2}=8$.
当$x=48$时,$32-48<0$,不符合题意,舍去,
$\therefore x=8$.
答:小路的宽为8m.
设小路的宽为x m.
根据题意,得$(32-x)(24-x)=\frac {1}{2}×32×24$,
即$x^{2}-56x+384=0$,
解得$x_{1}=48,x_{2}=8$.
当$x=48$时,$32-48<0$,不符合题意,舍去,
$\therefore x=8$.
答:小路的宽为8m.
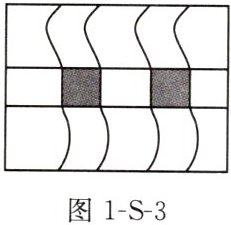
活动三:如图 1-S-3,在一块长是 32 m、宽是 24 m 的矩形绿地内,开辟出两条形状完全相同的弯曲小路和一条水平小路,然后在剩余的绿地上开辟花圃,使花圃的面积等于矩形面积的一半,那么小路的宽度应为多少米? (所有小路的宽度均相等,结果精确到 0.1 m.参考数据:$\sqrt {13}\approx 3.61$)

答案:
解:设小路的宽为x m.
根据题意,得$(32-2x)(24-x)=\frac {1}{2}×32×24$,
即$x^{2}-40x+192=0$,
解得$x_{1}=20-4\sqrt {13},x_{2}=20+4\sqrt {13}$(舍去),
$\because 20-4\sqrt {13}\approx 20-4×3.61=5.56\approx 5.6$.
$\therefore$小路的宽约为5.6m.
根据题意,得$(32-2x)(24-x)=\frac {1}{2}×32×24$,
即$x^{2}-40x+192=0$,
解得$x_{1}=20-4\sqrt {13},x_{2}=20+4\sqrt {13}$(舍去),
$\because 20-4\sqrt {13}\approx 20-4×3.61=5.56\approx 5.6$.
$\therefore$小路的宽约为5.6m.
查看更多完整答案,请扫码查看


