《2025年全品学练考九年级数学上册苏科版江苏专版》

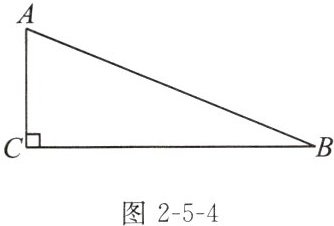
例2 如图2-5-4,在Rt△ABC中,∠C= 90°,AC= 5,AB= 13,以点C为圆心作⊙C.
(1)若⊙C与直线AB相切,求⊙C的半径r的值；
(2)若⊙C与直线AB相交,求⊙C的半径r的取值范围；
(3)若⊙C与线段AB有两个交点,求⊙C的半径r的取值范围.

答案：
(1)60/13
(2)r ＞ 60/13
(3)60/13 ＜ r ≤ 5

总结

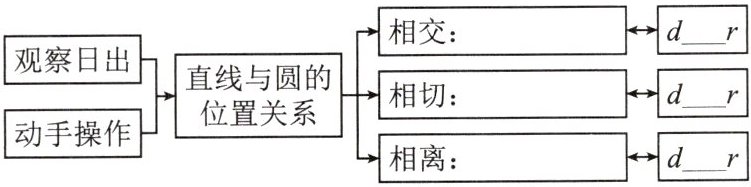
答案： 1. 首先明确直线与圆位置关系的定义：
设圆的半径为$r$，圆心到直线的距离为$d$。
当直线与圆相交时：
直线与圆有两个公共点。根据直线与圆位置关系的判定，此时$d\lt r$。
当直线与圆相切时：
直线与圆有一个公共点。根据直线与圆位置关系的判定，此时$d = r$。
当直线与圆相离时：
直线与圆没有公共点。根据直线与圆位置关系的判定，此时$d\gt r$。
2. 然后填写内容：
相交：直线与圆有两个公共点，$d\lt r$；
相切：直线与圆有一个公共点，$d = r$；
相离：直线与圆没有公共点，$d\gt r$。
故答案依次为：直线与圆有两个公共点；$\lt$；直线与圆有一个公共点；$=$；直线与圆没有公共点；$\gt$。

反思
直线与圆的位置关系中的d与点和圆的位置关系中的d,两者有何区别与联系？

答案： 解:区别:直线与圆的位置关系中的d是圆心到直线的距离，指的是垂线段的长度。
点和圆的位置关系中的d指的是点与圆心两点之间的距离。
联系:直线与圆的位置关系中的d，也可以理解为垂足与圆心的距离，因此直线与圆的位置关系也取决于垂足与圆的位置关系，即当垂足在圆外时，直线与圆的位置关系是相离；当垂足在圆上时，直线与圆的位置关系是相切；当垂足在圆内时，直线与圆的位置关系是相交。

观察思考
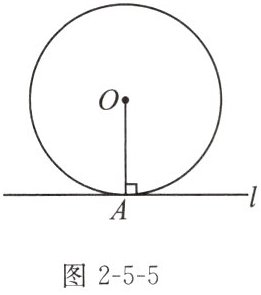
如图2-5-5,在$\odot O$中,经过半径OA的外端点A,作直线$l\perp OA$,直线l与$\odot O$有怎样的位置关系？

答案： 解:直线 l 与⊙O 相切.