《2025年全品学练考九年级数学上册苏科版江苏专版》

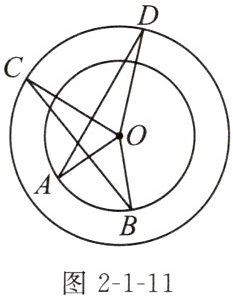
例2 (教材典题)如图2-1-11,点A,B和点C,D分别在以点O为圆心的两个同心圆上,且$∠AOB= ∠COD$.$∠C与∠D$相等吗? 为什么?

答案： 解：$∠C$与$∠D$相等.理由：
$\because ∠AOB = ∠COD$，
$\therefore ∠BOC = ∠AOD$.
又$\because OB = OA,OC = OD$（同圆的半径相等），
$\therefore △BOC ≌ △AOD$，
$\therefore ∠C = ∠D$.

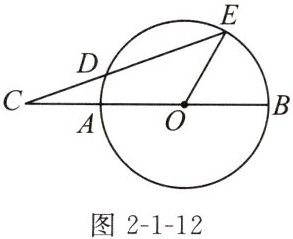
例3 (教材典题)如图2-1-12,AB是$\odot O$的直径,C是BA延长线上一点,点D在$\odot O$上,且$CD= OA$,CD的延长线交$\odot O$于点E.若$∠C= 20^{\circ }$,求$∠BOE$的度数.

答案： $60^{\circ}$

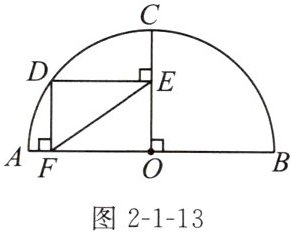
例4 如图2-1-13,半圆O的直径$AB= 8$,半径$OC⊥AB$,D为弧AC上一点,$DE⊥OC,DF⊥OA$,垂足分别为E,F,求EF的长.

答案：
解：$\because AB = 8,\therefore OA = OB = 4$.
如图，连接 OD.
$\because OC⊥AB,DE⊥OC,DF⊥OA$，
$\therefore ∠AOC = ∠DEO = ∠DFO = 90^{\circ}$，
$\therefore$ 四边形 DEOF 是矩形，
$\therefore EF = OD$.
$\because OD = OA,\therefore EF = OA = 4$.