动手操作
将方程$x^{2}+2x-24= 0$变形为
图示如图1-2-1:
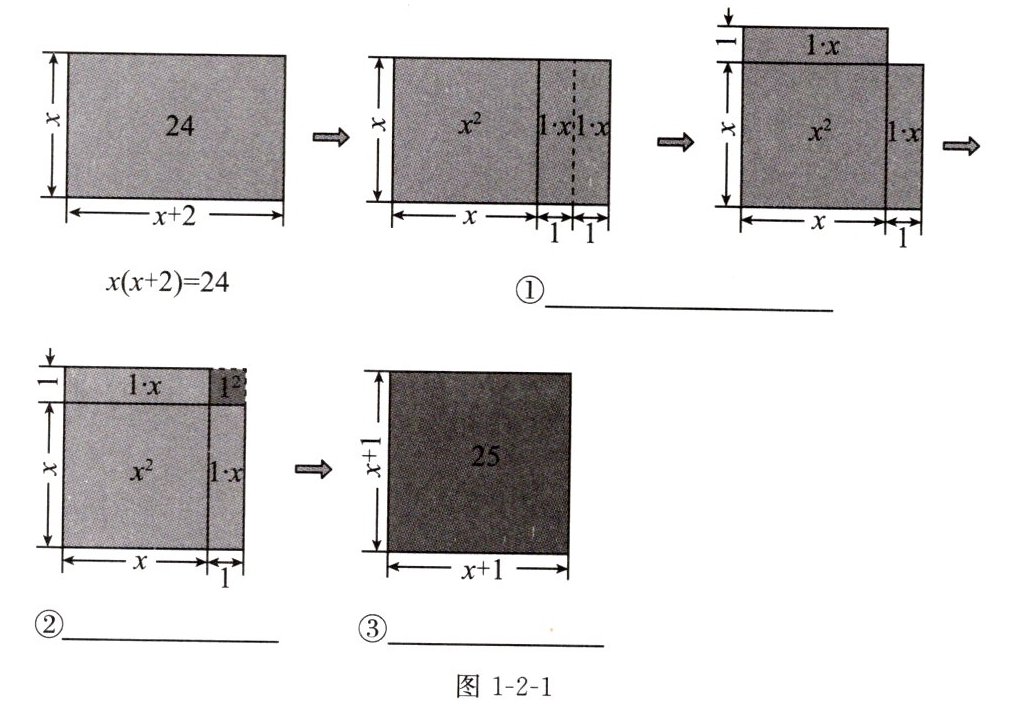
请在图中横线处补全“拼成一个正方形”过程的等式.
将方程$x^{2}+2x-24= 0$变形为
① $x^{2}+2x=24$
,即$x(x+2)= 24$.配方的过程可以看成将一个长是$(x+2)$、宽是x、面积是24的矩形割补成一个正方形.图示如图1-2-1:

请在图中横线处补全“拼成一个正方形”过程的等式.
② $x^{2}+2x+1^{2}=24+1^{2}$
③ $(x+1)^{2}=25$
答案:
① $x^{2}+2x=24$ ② $x^{2}+2x+1^{2}=24+1^{2}$ ③ $(x+1)^{2}=25$
反思
用配方法解方程:$x^{2}+bx+c= 0(b^{2}-4c≥0)$.
用配方法解方程:$x^{2}+bx+c= 0(b^{2}-4c≥0)$.
答案:
$x_{1}=\frac{-b+\sqrt{b^{2}-4c}}{2},x_{2}=\frac{-b-\sqrt{b^{2}-4c}}{2}$
用配方法解下列方程:
(1)$x^{2}-6x-16= 0;$ (2)$x^{2}+3x-2= 0.$
(1)$x^{2}-6x-16= 0;$ (2)$x^{2}+3x-2= 0.$
答案:
(1)$x_{1}=8,x_{2}=-2$
(2)$x_{1}=-\frac {3}{2}+\frac {\sqrt {17}}{2},x_{2}=-\frac {3}{2}-\frac {\sqrt {17}}{2}$
(1)$x_{1}=8,x_{2}=-2$
(2)$x_{1}=-\frac {3}{2}+\frac {\sqrt {17}}{2},x_{2}=-\frac {3}{2}-\frac {\sqrt {17}}{2}$
查看更多完整答案,请扫码查看


