《2025年全品学练考九年级数学上册苏科版江苏专版》

归纳 圆周角的度数等于它所对弧上的圆心角度数的一半.

答案： 一半

3. 如图2-4-5,A,B,C为$\odot O$上的三点,$A_{1},A_{2},A_{3}为\odot O$上异于它们的三点,则$∠A_{1},∠A_{2},∠A_{3},∠A与∠BOC$的数量关系为$∠A_{1} = ∠A_{2} = ∠A_{3} = ∠A = \frac{1}{2}∠BOC$.

答案： $∠A_{1} = ∠A_{2} = ∠A_{3} = ∠A = \frac{1}{2}∠BOC$

例2 (教材典题)如图2-4-6,$\odot O$的弦AB,DC的延长线相交于点E,$∠AOD= 150^{\circ },\overset{\frown }{BC}为70^{\circ }$.求$∠ABD,∠AED$的度数.

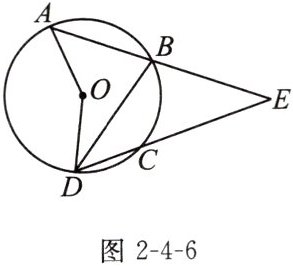
答案： $∠ABD = 75^{\circ}$,$∠AED = 40^{\circ}$

如图2-4-7,已知线段MN,求作点P,使$∠MPN= 135^{\circ }$.
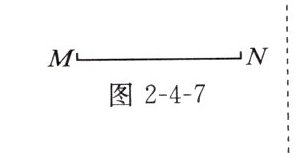
(尺规作图,保留作图痕迹,写出必要的文字说明)

答案：
解:如图.①分别以点M,N为圆心,大于$\frac{1}{2}MN$的长为半径画弧交于两点A,B,作直线AB交MN于点C;
②以点C为圆心,CM长为半径作弧交直线AB于点O,连接MO;
③以点O为圆心,OM长为半径作$\odot O$;
④在劣弧MN(不含端点)上任取一点P,点P即为所求.