《2025年全品学练考九年级数学上册苏科版江苏专版》

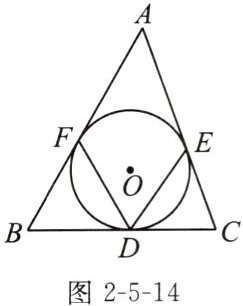
例1(教材典题)如图2-5-14,⊙O是△ABC的内切圆,切点分别为D,E,F,∠B= 60°,∠C= 70°. 求∠EDF的度数.

答案： 65°

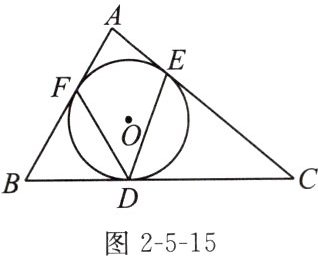
变式 如图2-5-15,⊙O是△ABC的内切圆,切点分别为D,E,F,若∠FDE= 50°,求∠A的度数.

答案： 80°

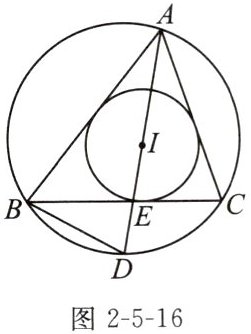
例2 如图2-5-16,在△ABC中,点I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,与BC相交于点E,连接DB. 求证：DI= DB.

答案： 证明:如图，连接BI。
∵点I是△ABC的内心，
∴∠BAI=∠CAI，∠ABI=∠CBI。
又
∵∠DBI=∠CBI+∠DBC，∠DIB=∠ABI+∠BAI，∠DBC=∠DAC=∠BAI，
∴∠DBI=∠DIB，
∴DI=DB。

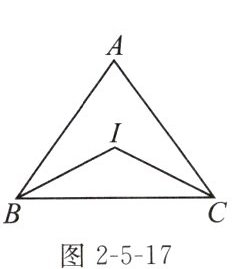
|如图2-5-17,已知I是△ABC内一点. 若∠BIC= 90°+$\frac{1}{2}$∠BAC且BI平分∠ABC.|
|求证：点I是△ABC的内心.|

答案： 解：
1. 设$\angle ABC = 2x$，因为$BI$平分$\angle ABC$，所以$\angle IBC=x$。
2. 在$\triangle BIC$中，根据三角形内角和定理$\angle BIC+\angle IBC+\angle ICB = 180^{\circ}$，已知$\angle BIC=90^{\circ}+\frac{1}{2}\angle BAC$，则$\angle ICB=180^{\circ}-\angle BIC - \angle IBC$。
把$\angle BIC=90^{\circ}+\frac{1}{2}\angle BAC$和$\angle IBC = x$代入可得：$\angle ICB=180^{\circ}-\left(90^{\circ}+\frac{1}{2}\angle BAC\right)-x=90^{\circ}-\frac{1}{2}\angle BAC - x$。
3. 在$\triangle ABC$中，根据三角形内角和定理$\angle ABC+\angle BAC+\angle ACB = 180^{\circ}$，即$2x+\angle BAC+\angle ACB = 180^{\circ}$，所以$\angle ACB=180^{\circ}-\angle BAC - 2x$。
设$CI$平分$\angle ACB$，则$\angle ICB=\frac{1}{2}\angle ACB$。
把$\angle ACB=180^{\circ}-\angle BAC - 2x$代入$\angle ICB=\frac{1}{2}\angle ACB$得：$\angle ICB=\frac{1}{2}(180^{\circ}-\angle BAC - 2x)=90^{\circ}-\frac{1}{2}\angle BAC - x$，这与前面求出的$\angle ICB$表达式一致，所以$CI$平分$\angle ACB$。
4. 因为$BI$平分$\angle ABC$，$CI$平分$\angle ACB$，根据三角形内心的定义（三角形三条角平分线的交点叫三角形的内心），所以点$I$是$\triangle ABC$的内心。
综上，点$I$是$\triangle ABC$的内心得证。