《2025年学霸题中题九年级物理上册苏科版》

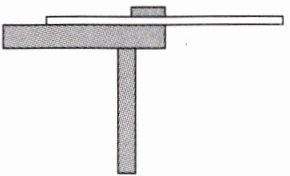
15. 如图所示,刻度尺的中间位置紧贴桌子边缘,将橡皮放在刻度尺上,其右端与桌子边缘齐平,若橡皮的质量为$m_1,$刻度尺的质量为$m_2,$橡皮的长为l,当水平向右缓慢推动刻度尺的距离超过$\frac {m_{1}l}{2(m_{1}+m_{2})}$时,刻度尺会翻倒。

答案： $\frac {m_{1}l}{2(m_{1}+m_{2})}$解析:当刻度尺刚好没有翻倒时,则以桌子边缘为支点,由于橡皮和刻度尺的重心在物体的几何中心上,则水平向右缓缓推动刻度尺的距离为刻度尺重力的力臂$L_{2}$,橡皮重力的力臂为$L_{1}=\frac {1}{2}l - L_{2}$,根据杠杆的平衡条件可得$G_{1}L_{1}=G_{2}L_{2}$,即$m_{1}g(\frac {1}{2}l - L_{2}) = m_{2}g×L_{2}$,解得$L_{2}=\frac {m_{1}l}{2(m_{1}+m_{2})}.$

16. 图甲是脚踏式翻盖垃圾桶的实物图,翻盖由两个杠杆组合而成,图乙为两水平杠杆$AO_1B、$$DCO_2$组合的示意图。已知桶盖重5 N,重心位于DC中点的正上方$,AO_1= 30 cm,O_1B= 20 cm,$桶盖和连接杆的尺寸如图乙所示,脚踏杆$AO_1B$和竖直连接杆BC的质量不计。

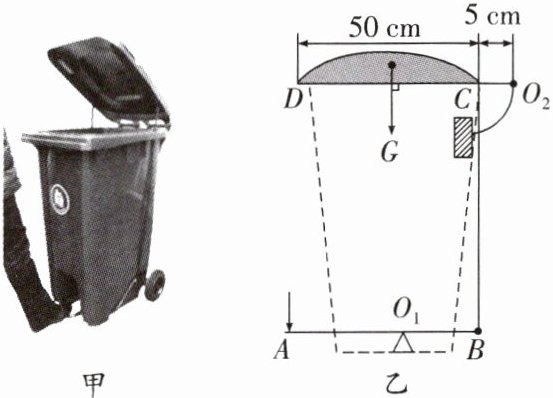
(1)杠杆$AO_1B$是省力(填“省力”或“费力”)杠杆。
(2)若要把桶盖翻开,脚对踏板A处的压力至少为20N。

答案：
(1)省力
(2)20 解析:
(1)杠杆$AO_{1}B$支点为$O_{1}$,动力在 A 点处,阻力在 B 点处,作用力在竖直方向上,此时动力臂大于阻力臂,故此杠杆为省力杠杆.
(2)如题图所示,在杠杆$DCO_{2}$中,阻力臂为$l_{1}=\frac {1}{2}DC + CO_{2}=\frac {1}{2}×50cm + 5cm = 30cm$,动力臂为$l_{2}=5cm$,根据杠杆平衡条件可得 C 点处作用力为$F_{C}=\frac {Gl_{1}}{l_{2}}=\frac {5N×30cm}{5cm}=30N$.若要把桶盖翻开,根据杠杆平衡条件,在杠杆$AO_{1}B$中,脚对踏板 A 处的压力至少为$F_{A}=\frac {F_{C}\cdot O_{1}B}{O_{1}A}=\frac {30N×20cm}{30cm}=20N.$

17. 新素材 创新装置 (2024·无锡天一学校期中)图甲是一款压饺子皮的工具,使用时压杆可以看作一个杠杆。图乙是简化示意图,图中O为支点$,F_2$是压杆上B点在下压时受到的阻力。请在乙图上画出阻力臂$l_2、$作用在杠杆A点需要施加的最小动力$F_1。$

答案：
如图所示
　　　　　　　　

18. (2025·南京建邺区期中)如图所示为可调节式落地灯,高为0.6 m的立柱OA与底座为一整体。重心为O,总重为100 N,O到底座边缘最远的距离OD为0.2 m,轻质杆AB既可绕A点转动又可以伸缩调节长度,最长可调节为2 m。立柱OA与灯中轴线的距离称为跨度,若灯的质量为2 kg,则该灯的最大跨度为 m；若将B点到地面的高度调为1.5 m,则轻质杆AB最长可调为 m；要增加灯的最大跨度,可有 和 等方法。(g取10 N/kg)

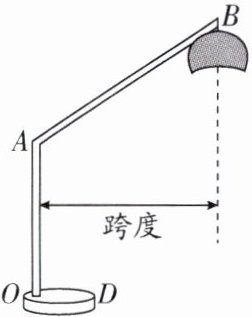
答案：
1.2 1.5 增大底座配重 减小灯的质量 解析:根据题目意思画出动力和动力臂,阻力和阻力臂,如图所示.动力为灯的重力 20 N,阻力为总重 100 N,阻力臂$l_{1}$为0.2 m,根据杠杆平衡条件$F_{1}l_{1}=F_{2}l_{2}$,求出动力臂$l_{2}$,再计算跨度为$L_{跨度}=l_{1}+l_{2}=l_{1}+\frac {F_{1}l_{1}}{F_{2}}=0.2m+\frac {100N×0.2m}{20N}=1.2m$;根据题目意思可知,在$\triangle ABC$中$l_{AC}=1.2m$,$l_{BC}=1.5m - 0.6m = 0.9m$,根据勾股定理求得$l_{AB}=\sqrt {l_{AC}^{2}+l_{BC}^{2}}=\sqrt {(1.2m)^{2}+(0.9m)^{2}}=1.5m$;根据题意要让灯在保持平衡前提下增加灯的最大跨度,由杠杆平衡条件$F_{1}l_{1}=F_{2}l_{2}$,可以增大阻力大小,即增大底座配重,或者减小动力大小,即减小灯的质量.
　　　　　　　　

19. 核心素养 科学思维 如图是测量质量的磅秤的构造示意图。AB是一根不等臂杠杆,支点为$O_1,CD$和EF都是可看作杠杆的两块平板,分别以$O_2、$$O_3$为支点,CD板用竖直杆HC悬于H点,EF板用竖直杆EB悬于B点,EB穿过CD板的小孔,且与CD板无摩擦。(除重物G和砝码P,其他物件重力不计)
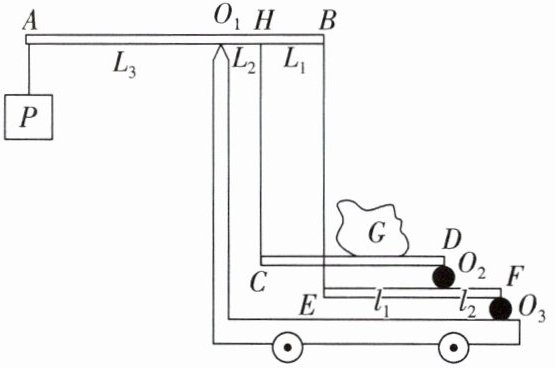
(1)重物G放置在称台CD板上,则重物G的摆放位置对测量结果无(填“有”或“无”)影响。
(2)若HB、$O_1H、$$O_1A、$$O_2E、$$O_2F$的长度分别用$L_1、$$L_2、$$L_3、$$l_1、$$l_2$表示,而且$L_1= 10 cm,L_2= 1 cm,L_3= 60 cm,l_1= 40 cm,l_2= 4 cm。$磅秤平衡时,砝码P重力Gₚ= 50 N。则秤台CD上的重物的重力G为多少？

3000N

答案：
(1)无
(2)3000N
解析:
(1)CD 板自身重力不计,受到物体 G 的压力,C 端杆的拉力$F_{C}$,D 端向上的支持力$F_{D}$,由受力平衡有:$G = F_{C}+F_{D}$
对于杠杆 AB,由平衡条件有:$G_{p}L_{3}=F_{C}L_{2}+F_{B}(L_{1}+L_{2})$;
对于杠杆 EF,由平衡条件有:$F_{E}(l_{1}+l_{2})=F_{D}l_{2}$;
因为力的作用是相互的,且杆的重力忽略不计,故$F_{E}$与$F_{C}$大小相等,$F_{B}$与$F_{D}$大小相等,代入上式,可得:
$F_{D}\frac {l_{2}(L_{1}+L_{2})}{l_{1}+l_{2}}+F_{C}L_{2}=G_{p}L_{3}$;
将$L_{1}=10cm$,$L_{2}=1cm$,$L_{3}=60cm$,$l_{1}=40cm$,$l_{2}=4cm$代入,可得$F_{D}+F_{C}=60G_{p}$,而$G = F_{C}+F_{D}$,故有$G = 60G_{p}$,这一等式成立与物体 G 摆放在 CD 板上的位置无关,所以物体 G 的摆放位置对测量结果无影响.
(2)根据
(1)的结论,代入数据$G_{p}=50N$,解得:$G = 3000N$.