《2025年学霸题中题九年级物理上册苏科版》

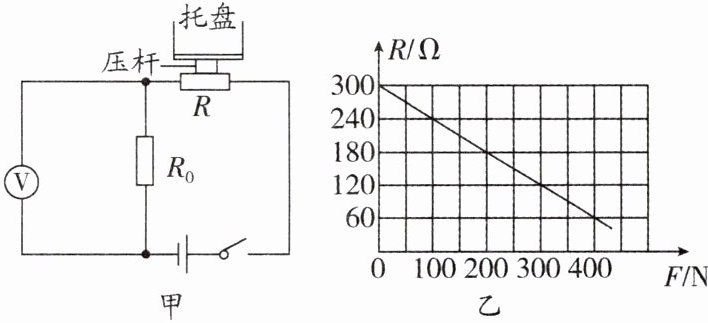
6. (2024·连云港二模)图甲是某校实践活动小组设计的电子秤的结构原理图,通过改写电压表的表盘数值后可直接读出所称量物体的质量.已知电阻$R_{0}= 60Ω$,电压表的量程为0~3V,压力传感器R的阻值与所受压力变化的图像如图乙所示,设托盘和压杆的质量可以忽略不计,电源电压保持6V恒定不变,g取10N/kg.
(1)电子秤的最大称量值是多大?
(2)"0 kg"应标记在表盘上的哪个刻度线处?
(3)如果保持电子秤结构和电压表量程不变,使电子秤的量程变为0~30 kg,应将电阻$R_{0}更换为多大的电阻R_{1}$?

答案：
(1)40 kg
(2)1 V
(3)120 Ω
解析:
(1)根据电路图可知,压力传感器R与定值电阻R₀串联,电压表测量R₀两端的电压;当所称量物体的质量增加时,压力传感器受到的压力增大;由R-F图像可知,压力增大时,压力传感器的阻值减小,由串联分压原理,定值电阻R₀两端的电压变大,即电压表的示数变大;则当电子秤所测质量最大时,对应的电压表示数达到最大值;所以,根据电压表的量程可知,当定值电阻R₀两端的电压为U₀最大=3 V时,电子秤达到最大称量值,电路中的电流最大为I_最大=$\frac{U_{0\text{最大}}}{R_0}$=$\frac{3\ \text{V}}{60\ \Omega}$=0.05 A,压力传感器R两端分得的电压U_R=U-U₀=6 V-3 V=3 V,压力传感器R的阻值R=$\frac{U_R}{I_{\text{最大}}}$=$\frac{3\ \text{V}}{0.05\ \text{A}}$=60 Ω,由题图乙可知,此时压力传感器R受到的压力为400 N,所测物体的最大重力为G_物最大=F=400 N,由G=mg可得,该电子秤的最大称量值m_物最大=$\frac{G_{\text{物最大}}}{g}$=$\frac{400\ \text{N}}{10\ \text{N/kg}}$=40 kg.
(2)由题图乙可知,当压力传感器R不受压力时,R的阻值最大,由图像可知R'=300 Ω,电路中的电流I=$\frac{U}{R_0+R'}$=$\frac{6\ \text{V}}{60\ \Omega+300\ \Omega}$=$\frac{1}{60}$ A,电压表的示数U₀=IR₀=$\frac{1}{60}$ A×60 Ω=1 V,所以“0 kg”应标记在表盘上的“1 V”刻度线处.
(3)使电子秤的量程变为0~30 kg,则压力传感器R受到的最大压力为F_最大=G'=m'g=30 kg×10 N/kg=300 N,由题图乙可知,此时压力传感器阻值为120 Ω,若电子秤结构和电压表量程不变时,使电子秤的量程变为0~30 kg,应将电阻R₀更换为更大阻值的电阻R₁,即当压力传感器阻值达到最小120 Ω时,此时更换后的电阻R₁两端的电压U_R₁=3 V不变,由于压力传感器电阻R''与R₁串联,由分压原理可得,压力传感器分得的最大电压U_R''=U-U_R₁=6 V-3 V=3 V,所以由串联电路电压特点得$\frac{R_1}{R''}$=$\frac{U_{R_1}}{U_{R''}}$,即$\frac{R_1}{120\ \Omega}$=$\frac{3\ \text{V}}{3\ \text{V}}$,解得R₁=120 Ω.

7. (2024·北京中考)图甲为自动气象站中的测温装置,它的测温电路可简化为图乙,其中的"恒流源"是一个特殊电源,电流大小由电源内部结构决定,当电阻R变化时,通过R的电流大小保持不变.电阻R的阻值随温度的变化规律如图丙所示,通过数字电压表的示数可反映环境的温度.某次环境温度从20℃上升到30℃,电压表的示数变化了8mV.当温度的变化值相同时,电压表示数的变化值越大,该测温装置的灵敏度越高.下列说法正确的是(C)
A.每升高1℃,R的阻值增大1.65Ω

B.通过R的电流为20mA
C.环境温度为20℃时,电压表的示数为216mV
D.若要增大该测温装置的灵敏度,可换一个电流值更小的恒流源

答案： C 解析:A.由图丙可知,温度升高20 ℃,电阻增大8 Ω,则每升高1 ℃,R的阻值增大$\frac{8\ \Omega}{20}$=0.4 Ω,故A错误;BC.由图丙可知,当t=20 ℃时,R₁=108 Ω,由欧姆定律可知,通过R的电流I=$\frac{U_1}{R_1}$=$\frac{U_1}{108\ \Omega}$,当t=30 ℃时R₂=R₁+0.4 Ω/℃×(30 ℃-20 ℃)=112 Ω,则通过R的电流为I₂=$\frac{U_2}{R_2}$=$\frac{U_2}{112\ \Omega}$.由题意可知,当电阻R变化时,通过R的电流大小保持不变,环境温度从20 ℃上升到30 ℃,电阻变大,由U=IR可知,电压表的示数会增大,因电压表的示数变化了8 mV,即U₂=U₁+0.008 V,因电流不变,则I₁=I₂,即$\frac{U_1}{108\ \Omega}$=$\frac{U_1+0.008\ \text{V}}{112\ \Omega}$,解得U₁=0.216 V=216 mV,I₁=I₂=2 mA,故B错误,C正确;D.由ΔU=IΔR可知,阻值变化量相同时,电流越大,电压表示数变化值越大,因此若要增大该测温装置的灵敏度,可换一个电流值更大的恒流源.故D错误.故选C.

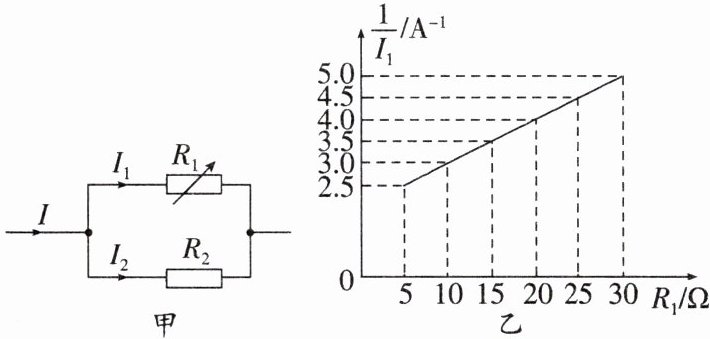
8. 如图甲所示,$R_{2}$为定值电阻,$R_{1}$为可变电阻,其阻值可调可读,保持干路电流I不变.
(1)若该电路接入电压为6V的电源两端,定值电阻$R_{2}= 15Ω$,干路电流I= 1A,求可变电阻$R_{1}$的阻值.
(2)已知通过可变电阻$R_{1}的电流的倒数\frac{1}{I_{1}}与其阻值R_{1}$的关系图线如图乙所示,试求:
①定值电阻$R_{2}$;
②干路电流I的值.(提示:并联电路两端电压不是定值)

答案：
(1)10 Ω
(2)①20 Ω ②0.5 A
解析:
(1)通过电阻R₂的电流为I₂=$\frac{U}{R_2}$=$\frac{6\ \text{V}}{15\ \Omega}$=0.4 A,
由并联电路电流的规律知通过电阻R₁的电流为I₁=I-I₂=1 A-0.4 A=0.6 A,
可变电阻R₁的阻值为R₁=$\frac{U}{I_1}$=$\frac{6\ \text{V}}{0.6\ \text{A}}$=10 Ω.
(2)①由图乙知道,当R₁=5 Ω时,通过R₁的电流为I₁'=$\frac{1}{2.5}$ A=0.4 A,
此时的电源电压为U=I₁' R₁=0.4 A×5 Ω=2 V,
根据并联电路电流规律可知此时通过定值电阻的电流为I₂'=I-I₁'=I-0.4 A.
根据欧姆定律知,定值电阻的阻值为R₂=$\frac{U}{I_2'}$=$\frac{2\ \text{V}}{I-0.4\ \text{A}}$…①
当R₁'=20 Ω时,通过R₁的电流I₁''=$\frac{1}{4}$ A=0.25 A,
此时的电源电压为U'=I₁'' R₁'=0.25 A×20 Ω=5 V,
根据并联电路电流规律可知此时通过定值电阻的电流为I₂''=I-I₁''=I-0.25 A,
根据欧姆定律可得定值电阻的阻值为R₂=$\frac{U'}{I_2''}$=$\frac{5\ \text{V}}{I-0.25\ \text{A}}$…②
①②联立可得I=0.5 A,R₂=20 Ω.