《2025年学霸题中题九年级物理上册苏科版》

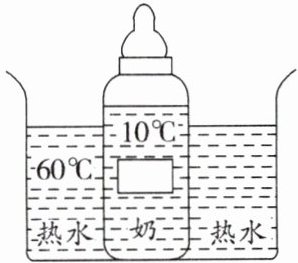
1. (2024·常州二十四中期中)由于天气寒冷,吃早饭时妈妈要用热水给小明加热 250 g 瓶装牛奶,如图所示,要使这瓶牛奶的温度由10°C最终升高到50°C,水的比热容为$4.2×10^3J/(kg·°C),$牛奶的比热容为$2.1×10^3J/(kg·°C),$不计热量损失,求：
(1)牛奶需要吸收多少热量？
(2)妈妈至少需要60°C的热水多少千克？
(3)如果实际过程中,为了达到效果,妈妈消耗了1 kg、70°C的热水,那么这个过程中热传递的效率是多少？

答案： $1. $　　
$(1)2.1×10⁴ J $　　
$(2)0.5 kg $　　
$(3)25\%$　　
解析$:$　　
$(1)$牛奶吸收的热量　　
$Q_{吸1}=c_{牛奶}m_{牛奶}(t-t_{0})=2.1×10³ J/(kg·℃)×250×10⁻³ kg×(50 ℃-10 ℃)=2.1×10⁴ J.$　　
$(2)$不计热量损失$,$因此　　
$Q_{放}=Q_{吸1}=2.1×10⁴ J,$　　
则至少需要$60 ℃$的热水　　
$m_{水}=Q_{放}/(c_{水}Δt_{水})=2.1×10⁴ J/(4.2×10³ J/(kg·℃)×(60 ℃-50 ℃))=0.5 kg.$　　
$(3)1$千克$70 ℃$的热水放出的热量为　　
$Q_{放1}=c_{水}m_{水1}(t₁-t)=4.2×10³ J/(kg·℃)×1 kg×(70 ℃-50 ℃)=8.4×10⁴ J,$　　
热传递的效率　　
$η=Q_{吸1}/Q_{放1}×100\%=2.1×10⁴ J/8.4×10⁴ J×100\%=25\%.$　　

2. (2024·苏州高新区期中)杭州亚运会首次使用废碳再生的绿色零碳甲醇作为主火炬塔燃料,已知当地气压为标准大气压,水的比热容是c水$= 4.2×10^3J/(kg·°C),$甲醇的热值约为$2.3×10^7J/kg,$天然气的热值为$4.2×10^7J/m^3,$求：
(1)完全燃烧8.4 kg甲醇和完全燃烧多少立方米的天然气放出的热量相等？
(2)若8.4 kg甲醇完全燃烧释放的热量有80%被水吸收,可以使质量是2.3 t、初温是35°C的水,温度上升到多少摄氏度？

答案： $2. $　　
$(1)4.6 m³ $　　
$(2)51 ℃$　　
解析$:$　　
$(1)$完全燃烧$8.4 kg$甲醇放出的热量　　
$Q_{放甲醇}=m_{甲醇}q_{甲醇}=8.4 kg×2.3×10⁷ J/kg=1.932×10⁸ J,$　　
则放出$1.932×10⁸ J$热量需要天然气　　
$V_{天然气}=Q_{放}/q_{天然气}=1.932×10⁸ J/(4.2×10⁷ J/m³)=4.6 m³.$　　
$(2)$甲醇完全燃烧释放的热量有$80\%$被水吸收$,$则水吸收的热量为　　
$Q_{吸}=ηQ_{放甲醇}=1.932×10⁸ J×80\%=1.5456×10⁸ J,$　　
使质量是$2.3 t、$初温是$35 ℃$的水温度上升的温度为　　
$Δt=Q_{吸}/(c_{水}m)=1.5456×10⁸ J/(4.2×10³ J/(kg·℃)×2.3×10³ kg)=16 ℃,$　　
水最终温度上升到　　
$t=t₀+Δt=35 ℃+16 ℃=51 ℃.$　　

3. 如图甲是小明家用的燃气热水器,图乙是连接在热水器上的一个混水阀。若将混水阀开关调到O位置左边并抬起把手,热水器自动点火,天然气燃烧,水龙头出热水；往O点右边调出冷水,按下把手则停止出水。小明在某次使用热水器时,把热水器的出水温度设定为44°C,此时测得从B管流进的自来水的流量为4 L/min,从C管流出的温度为40°C。小明检查燃气表,发现热水器工作1 min消耗天然气$0.08 m^3($自来水的温度为20°C,天然气的热值是$3.6×10^7J/m^3,$水的密度为$1×10^3kg/m^3)。$请解决下列问题：
(1)从A管流进混水阀的热水的流量为多少L/min？(计算过程中不计热损失)
(2)该热水器的加热效率是多少？

答案： $3. $　　
$(1)20 L/min $　　
$(2)70\% $解析$:$　　
$(1)$不计热损失$,$热水放出的热量全部被自来水吸收$,$热水放出的热量等于自来水吸收的热量$,$即$cm_{热}Δt₁=cm_{冷}Δt₂,$则$m_{热}Δt₁=m_{冷}Δt₂,$从$B$管流进的自来水的流量为$4 L/min,$即每分钟流进$B$管的冷水体积$V_{B}=4 L,$根据$ρ=m/V,$并将数据代入上式可得$ρ_{水}V_{A}×(44 ℃-40 ℃)=ρ_{水}V_{B}×(40 ℃-20 ℃),$解得$V_{A}=5V_{B}=5×4 L=20 L,$故从$A$管流进混水阀的热水的流量为$20 L/min.$　　
$(2)$热水器的出水温度设定为$44 ℃($即加热时水的末温$),$水加热前的初温为$20 ℃;$每分钟被热水器加热的水的体积为$V_{A}=20 L;$每分钟被热水器加热的水的质量为$m=ρ_{水}V_{A}=1×10³ kg/m³×20×10⁻³ m³=20 kg,$则热水器中水吸收的热量$Q_{吸}=cmΔt=4.2×10³ J/(kg·℃)×20 kg×(44 ℃-20 ℃)=2.016×10⁶ J,$天然气放出的热量为$Q_{放}=Vq=0.08 m³×3.6×10⁷ J/m³=2.88×10⁶ J,$则该热水器的加热效率为$η=Q_{吸}/Q_{放}×100\%=2.016×10⁶ J/2.88×10⁶ J×100\%=70\%.$