第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
9. 小红测量小灯泡的阻值,但发现电压表已损坏,于是找来一个电阻箱,设计如图甲所示电路,操作如下:①将待测小灯泡接入电路中M、N两点间,闭合开关,电流表示数为I;②取下小灯泡,将电阻箱接入M N两点间,调节电阻箱,使
电流表示数为I
,此时电阻箱示数如图乙所示,则小灯泡的阻值约为8.2
$ \Omega $.
答案:
9. 电流表示数为I 8.2 解析:①将待测的小灯泡接入电路中M、N两点间,闭合开关,电流表示数为I;②取下小灯泡,将电阻箱接入M N两点间,调节电阻箱,使电流表示数为I,则小灯泡电阻等于此时电阻箱接入电路的电阻,由图乙可知,电阻箱读数为8.2Ω,则小灯泡的阻值约为8.2Ω.
10. (2024·苏州中考)用如图所示电路测电阻 $ R_{x} $ 的阻值. 实验步骤如下: (1)将电压表接在B、C两点间,闭合开关,将滑动变阻器滑片移到b端,电阻箱R调为某一阻值$ R_{1} $,使电压表电流表示数为合适的值. (2)断开开关电压表右端由C点改接到D点. (3)闭合开关反复调节
实验步骤如下: (1)将电压表接在B、C两点间,闭合开关,将滑动变阻器滑片移到b端,电阻箱R调为某一阻值$ R_{1} $,使电压表电流表示数为合适的值. (2)断开开关电压表右端由C点改接到D点. (3)闭合开关反复调节
 实验步骤如下: (1)将电压表接在B、C两点间,闭合开关,将滑动变阻器滑片移到b端,电阻箱R调为某一阻值$ R_{1} $,使电压表电流表示数为合适的值. (2)断开开关电压表右端由C点改接到D点. (3)闭合开关反复调节
实验步骤如下: (1)将电压表接在B、C两点间,闭合开关,将滑动变阻器滑片移到b端,电阻箱R调为某一阻值$ R_{1} $,使电压表电流表示数为合适的值. (2)断开开关电压表右端由C点改接到D点. (3)闭合开关反复调节电阻箱和滑动变阻器
使两表的值与步骤(1)相同,此时电阻箱的阻值为$ R_{2} $. (4)待测电阻的阻值$ R_{x}= $$ R_{1}-R_{2} $
. (5)若操作无误,反复调节始终无法实现两表的值与步骤(1)相同,原因可能有:$ R_{1}<R_{x} $(或$ R_{1} $的阻值太小)
、滑动变阻器最大阻值小于$ R_{x} $(或滑动变阻器最大阻值不够大)(合理即可)
.
答案:
10.
(3)电阻箱和滑动变阻器
(4)$ R_{1}-R_{2} $
(5)$ R_{1}<R_{x} $(或$ R_{1} $的阻值太小) 滑动变阻器最大阻值小于$ R_{x} $(或滑动变阻器最大阻值不够大)(合理即可)
解析:
(3)闭合开关,反复调节电阻箱和滑动变阻器,使两表的示数与步骤
(1)中相同,此时电阻箱的阻值为$ R_{2} $.
(4)由题意可知,两次的电路电流相同,步骤
(3)中电阻箱$ R_{2} $和待测电阻$ R_{x} $两端总电压与步骤
(1)中电阻箱两端电压相同,由欧姆定律可知$\frac{U}{R_{2}+R_{x}}=\frac{U}{R_{1}} $,解得$ R_{x}=R_{1}-R_{2} $.
(5)由于电路电流相同,则电路总阻值相同,在步骤
(1)中,总阻值为$ R_{1}+ R_{\text{滑}} $(此时滑动变阻器接入阻值为0),在步骤
(3)中,总阻值为$ R_{2}+R_{x}+ R_{\text{滑}}' $,则有$ R_{1}=R_{2}+ R_{\text{滑}}' $…①,根据第
(4)问的分析得$ R_{1}-R_{2}=R_{x} $…②,联立①②式得$ R_{\text{滑}}'=R_{x} $…③,由此可得:若电阻箱第一次的阻值$ R_{1}<R_{x} $,则无法满足②式;若滑动变阻器的最大阻值小于$ R_{x} $,则无法满足③式.
重难点突破
该电路的原理是通过调节电阻箱和滑动变阻器,令第2次的$ R_{2}+R_{x} $等效替代第1次的$ R_{1} $,第一个关键点是两次的电路电流相等,从而得出电路的总电阻是不变的,第二个关键点是两次测量的电压相等,从而得出两次电压表所并联的电阻阻值相等.因此我们可以得出,在第2次测量中,电阻箱阻值减小了$ R_{x} $,滑动变阻器阻值增大了$ R_{x} $,若过程中无法实现两表的读数与步骤
(1)中相同,则表示电阻箱第一次的阻值$ R_{1} $过小,不足以使减小值为$ R_{x} $,或者滑动变阻器最大阻值不够大,不足以使增加值为$ R_{x} $.
(3)电阻箱和滑动变阻器
(4)$ R_{1}-R_{2} $
(5)$ R_{1}<R_{x} $(或$ R_{1} $的阻值太小) 滑动变阻器最大阻值小于$ R_{x} $(或滑动变阻器最大阻值不够大)(合理即可)
解析:
(3)闭合开关,反复调节电阻箱和滑动变阻器,使两表的示数与步骤
(1)中相同,此时电阻箱的阻值为$ R_{2} $.
(4)由题意可知,两次的电路电流相同,步骤
(3)中电阻箱$ R_{2} $和待测电阻$ R_{x} $两端总电压与步骤
(1)中电阻箱两端电压相同,由欧姆定律可知$\frac{U}{R_{2}+R_{x}}=\frac{U}{R_{1}} $,解得$ R_{x}=R_{1}-R_{2} $.
(5)由于电路电流相同,则电路总阻值相同,在步骤
(1)中,总阻值为$ R_{1}+ R_{\text{滑}} $(此时滑动变阻器接入阻值为0),在步骤
(3)中,总阻值为$ R_{2}+R_{x}+ R_{\text{滑}}' $,则有$ R_{1}=R_{2}+ R_{\text{滑}}' $…①,根据第
(4)问的分析得$ R_{1}-R_{2}=R_{x} $…②,联立①②式得$ R_{\text{滑}}'=R_{x} $…③,由此可得:若电阻箱第一次的阻值$ R_{1}<R_{x} $,则无法满足②式;若滑动变阻器的最大阻值小于$ R_{x} $,则无法满足③式.
重难点突破
该电路的原理是通过调节电阻箱和滑动变阻器,令第2次的$ R_{2}+R_{x} $等效替代第1次的$ R_{1} $,第一个关键点是两次的电路电流相等,从而得出电路的总电阻是不变的,第二个关键点是两次测量的电压相等,从而得出两次电压表所并联的电阻阻值相等.因此我们可以得出,在第2次测量中,电阻箱阻值减小了$ R_{x} $,滑动变阻器阻值增大了$ R_{x} $,若过程中无法实现两表的读数与步骤
(1)中相同,则表示电阻箱第一次的阻值$ R_{1} $过小,不足以使减小值为$ R_{x} $,或者滑动变阻器最大阻值不够大,不足以使增加值为$ R_{x} $.
11. 核心素养 科学探究 小华用电源(3 V)、电流表(0~0.6 A/0~3 A)、刻度尺、鳄鱼夹等器材,探究粗细均匀电阻丝的电阻与长度的关系,实验电路如图甲所示,测得数据如表:|序号|长度L/cm|电流I/A|

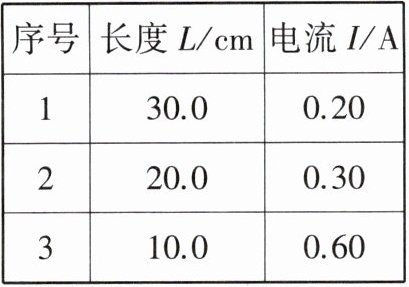
|1|30.0|0.20|
|2|20.0|0.30|
|3|10.0|0.60|(1)根据实验数据,可求得1 cm该电阻丝的电阻为______$ \Omega $. (2)小明在小华实验的基础上,利用该电阻丝测量未知电阻 $ R_{x} $ 的阻值(约10 $ \Omega $).①按图甲连好电路,闭合开关,在电阻丝上移动鳄鱼夹M,使电流表的示数为0.50 A. ②保持M位置不变,把 $ R_{x} $ 接入电路,如图乙所示.闭合开关,此时电流表的示数为0.20 A,请在虚线框内画出图乙的电路图,并求出此时 $ R_{x} $ 的电阻为______$ \Omega $. ③小明实验时电源的实际电压比3 V略低,则他测算出的电阻值______(填"偏大""偏小"或"不变"). ④为了消除因电源电压降低对电阻测量结果的影响,小明用原实验电路,改变测量方法就可以消除影响.其做法是: ⅰ.连接图甲电路,闭合开关,移动M使电流表的示数为0.20 A,记下M的位置A; ⅱ.把 $ R_{x} $ 接入电路,闭合开关,移动M使电流表示数为______A,记下M的位置B; ⅲ.用刻度尺量出AB间距离为L cm,则$ R_{x}= $______$ \Omega $.
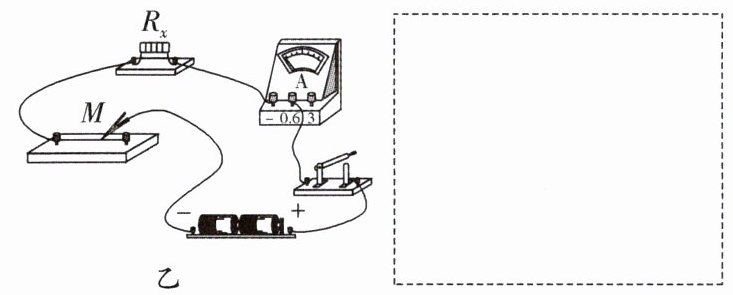


|1|30.0|0.20|
|2|20.0|0.30|
|3|10.0|0.60|(1)根据实验数据,可求得1 cm该电阻丝的电阻为______$ \Omega $. (2)小明在小华实验的基础上,利用该电阻丝测量未知电阻 $ R_{x} $ 的阻值(约10 $ \Omega $).①按图甲连好电路,闭合开关,在电阻丝上移动鳄鱼夹M,使电流表的示数为0.50 A. ②保持M位置不变,把 $ R_{x} $ 接入电路,如图乙所示.闭合开关,此时电流表的示数为0.20 A,请在虚线框内画出图乙的电路图,并求出此时 $ R_{x} $ 的电阻为______$ \Omega $. ③小明实验时电源的实际电压比3 V略低,则他测算出的电阻值______(填"偏大""偏小"或"不变"). ④为了消除因电源电压降低对电阻测量结果的影响,小明用原实验电路,改变测量方法就可以消除影响.其做法是: ⅰ.连接图甲电路,闭合开关,移动M使电流表的示数为0.20 A,记下M的位置A; ⅱ.把 $ R_{x} $ 接入电路,闭合开关,移动M使电流表示数为______A,记下M的位置B; ⅲ.用刻度尺量出AB间距离为L cm,则$ R_{x}= $______$ \Omega $.

答案:
11.
(1)0.5
(2)②见解析图 9 ③偏大 ④ⅱ 0.20 ⅲ 0.5L
解析:
(1)电源电压为3V,当长度为30cm时,电流的大小为0.2A,则接入的电阻为$ R_{1}=\frac{U}{I_{1}}=\frac{3\ \text{V}}{0.2\ \text{A}} = 15\ \Omega $,1 cm该电阻丝的电阻为$ R_{0}=\frac{R_{1}}{L_{1}}=\frac{15\ \Omega}{30}=0.5\ \Omega $.
(2)②根据实物图,依次画电源、开关、电流表、待测电阻、滑动变阻器,并用导线依次连接,如图所示.

当闭合开关,在电阻丝上移动鳄鱼夹M,使电流表的示数为0.50A,此时滑动变阻器的阻值为$ R_{2}=\frac{U}{I_{2}}=\frac{3\ \text{V}}{0.5\ \text{A}} = 6\ \Omega $.保持M位置不变,把$ R_{x} $接入电路,此待测电阻与滑动变阻器串联,电流表的示数为0.20A,则总电阻为$ R_{\text{总}}=\frac{U}{I_{3}}=\frac{3\ \text{V}}{0.2\ \text{A}} = 15\ \Omega $,待测电阻的阻值为$ R_{x}=R_{\text{总}}-R_{2}=15\ \Omega-6\ \Omega = 9\ \Omega $.
③待测电阻两端的电压为$ U_{0} $,电源电压为U,则滑动变阻器两端的电压为$ U_{\text{滑}}=U - U_{0} $,待测电阻与滑动变阻器的电阻之比为$\frac{U_{0}}{U_{\text{滑}}}=\frac{U_{0}}{U - U_{0}}=\frac{IR_{x}}{IR_{\text{滑}}}=\frac{R_{x}}{R_{\text{滑}}} $,则待测电阻为$ R_{x}=\frac{U_{0}R_{\text{滑}}}{U - U_{0}} $,电源电压偏小,故待测电阻测量值偏大.
④用等效替代的方法测量电阻.ⅰ. 连接图甲电路,闭合开关,移动M使电流表的示数为0.20A,记下M的位置A;ⅱ. 把$ R_{x} $接入电路,闭合开关,移动M使电流表示数为0.20A,记下M的位置B,电源电压一定,电流相同,故两次实验的总电阻相同;ⅲ. 用刻度尺量出AB间距离为L cm,则待测电阻的阻值即为AB间的电阻,每1 cm电阻为0.5Ω,故待测电阻的阻值为0.5LΩ.
技巧点拨
本题的实质就是自制一个能读出阻值的滑动变阻器,并利用该变阻器,运用等效替代法测未知电阻阻值.
11.
(1)0.5
(2)②见解析图 9 ③偏大 ④ⅱ 0.20 ⅲ 0.5L
解析:
(1)电源电压为3V,当长度为30cm时,电流的大小为0.2A,则接入的电阻为$ R_{1}=\frac{U}{I_{1}}=\frac{3\ \text{V}}{0.2\ \text{A}} = 15\ \Omega $,1 cm该电阻丝的电阻为$ R_{0}=\frac{R_{1}}{L_{1}}=\frac{15\ \Omega}{30}=0.5\ \Omega $.
(2)②根据实物图,依次画电源、开关、电流表、待测电阻、滑动变阻器,并用导线依次连接,如图所示.

当闭合开关,在电阻丝上移动鳄鱼夹M,使电流表的示数为0.50A,此时滑动变阻器的阻值为$ R_{2}=\frac{U}{I_{2}}=\frac{3\ \text{V}}{0.5\ \text{A}} = 6\ \Omega $.保持M位置不变,把$ R_{x} $接入电路,此待测电阻与滑动变阻器串联,电流表的示数为0.20A,则总电阻为$ R_{\text{总}}=\frac{U}{I_{3}}=\frac{3\ \text{V}}{0.2\ \text{A}} = 15\ \Omega $,待测电阻的阻值为$ R_{x}=R_{\text{总}}-R_{2}=15\ \Omega-6\ \Omega = 9\ \Omega $.
③待测电阻两端的电压为$ U_{0} $,电源电压为U,则滑动变阻器两端的电压为$ U_{\text{滑}}=U - U_{0} $,待测电阻与滑动变阻器的电阻之比为$\frac{U_{0}}{U_{\text{滑}}}=\frac{U_{0}}{U - U_{0}}=\frac{IR_{x}}{IR_{\text{滑}}}=\frac{R_{x}}{R_{\text{滑}}} $,则待测电阻为$ R_{x}=\frac{U_{0}R_{\text{滑}}}{U - U_{0}} $,电源电压偏小,故待测电阻测量值偏大.
④用等效替代的方法测量电阻.ⅰ. 连接图甲电路,闭合开关,移动M使电流表的示数为0.20A,记下M的位置A;ⅱ. 把$ R_{x} $接入电路,闭合开关,移动M使电流表示数为0.20A,记下M的位置B,电源电压一定,电流相同,故两次实验的总电阻相同;ⅲ. 用刻度尺量出AB间距离为L cm,则待测电阻的阻值即为AB间的电阻,每1 cm电阻为0.5Ω,故待测电阻的阻值为0.5LΩ.
技巧点拨
本题的实质就是自制一个能读出阻值的滑动变阻器,并利用该变阻器,运用等效替代法测未知电阻阻值.
查看更多完整答案,请扫码查看


