《2025年学霸题中题九年级物理上册苏科版》

16. 如图甲所示,有一质量为3 kg的正方体物块,在拉力F的作用下在水平面上做直线运动.拉力随时间变化速度随时间变化图像分别如图乙、丙所示,已知物块在2~4 s的运动距离为2 m.求:
(1)在2~4 s物块受到的摩擦力.
(2)在前6 s内,拉力F做的功.

答案：
(1)6 N
(2)42 J 解析:
(1)由图像可知物块在 4~6 s 做匀速直线运动,摩擦力 f 与拉力 F 大小相等,即 f = F = 6 N,物块运动过程压力和接触面粗糙程度不变,摩擦力不变.所以 2~4 s 物块受到的摩擦力 f' = f = 6 N.
(2)0~2 s 物块处于静止状态,拉力不做功,已知物块在 2~4 s 运动的距离 s' = A2 m,2~4 s 拉力 F 做的功 W' = F's' = 9 N×2 m = A18 J,物块在 4~6 s 内运动的距离 s = vt = 2 m/s×2 s = 4 m,4~6 s 拉力 F 做的功 W = Fs = 6 N×4 m = 24 J,前 6 s 拉力 F 做的功 W₈ₐₐ = W' + W = 18 J + 24 J = 42 J.

17. 新素材 创新装置 悠悠球是世界上较古老的玩具,它由轮与轴(含绕轴上的士线)两部分组成(如图甲).一悠悠球,轮半径为R,轴半径为r,线为细线,如图乙是玩悠悠球两种不同方式,小科用拉力F使球在水平方向匀速运动距离s,则下列说法正确的说(C)

A.两种方式拉力F做功均为Fs
B.a方式拉力F所做的功大于b方式拉力F所做的功
C.a方式拉力F所做的功小于b方式拉力F所做的功
D.无法判断

答案： C 解析:当悠悠球的轮向前滚动的距离为 s 时,已知轮半径为 R,轮滚动的圈数 n = $\frac{s}{2\pi R}$,轴滚动的圈数与轮相同,已知轴半径为 r,则轴向前滚动的距离 s' = n×2πr = $\frac{s}{2\pi R}$×2πr = $\frac{r}{R}$s,a 图,拉力 F 作用在轴的下端时,轴向前滚动会使细线“收缩”,拉力端实际移动的距离 s₁ = s - s' = s - $\frac{r}{R}$s = $(1 - \frac{r}{R})$s,F 做功大小 W₁ = Fs₁ = $(1 - \frac{r}{R})$Fs,b 图,拉力 F 作用在轴的上端时,轴向前滚动会使细线“拉长”,拉力端实际移动的距离 s₂ = s + s' = s + $\frac{r}{R}$s = $(1 + \frac{r}{R})$s,F 做功大小 W₂ = Fs₂ = $(1 + \frac{r}{R})$Fs,比较可得 W₁ ＜ W₂,故 C正确.

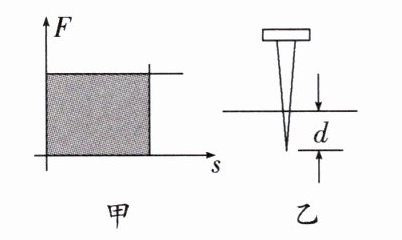
18. 核心素养 科学思维 图像法是物理学研究的重要方如图甲所示,在F-s图像中,图线与坐标轴合围面积即为功同理,如果Fs满足一次函数关系,则图线标轴合围成的三角形或梯形面积都可以作为做功的值现用铁锤把小钉钉入木板,设木板对小钉的阻力与钉进的深度成正比已知铁锤第一次敲钉子克服阻力做功为W,将钉子钉进深度d如图乙,如果第二次敲钉子时铁锤克服阻力做功仍为W,则第二次敲击将钉子钉进深度为 (用d表示).

答案：
($\sqrt{2}$ - 1)d 解析:由题可知,木板对小钉的阻力与钉进的深度成正比即 f = kd,作出该函数图像,图像下方的面积表示铁锤克服阻力做的功.如图所示: 由题意可知铁锤第一次克服阻力做功为 W,即 d 点左侧小三角形面积;第二次做功为 d~d'之间梯形面积,两次做功相同,则有:$\frac{1}{2}$df = $\frac{1}{2}$(f + f')(d' - d),结合 f = kd,解得 d' = $\sqrt{2}$d,则第二次敲击将钉子钉进的深度 $\Delta$d = d' - d = ($\sqrt{2}$ - 1)d.

19.(2025·苏州立达中学期中)一根长度为1.2 m、重为5 N金属棒AB置于水平地面上,用弹簧测力计始终沿竖直方向拉棒的B端使其缓慢匀速拉起,直至离开地面如图甲所示.


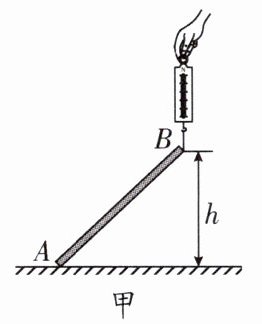
(1)在此过程中,弹簧测力计对棒所做功W B端离开地面的高度h关系如图乙所示,其中最合理的是 .
(2)在B端拉起过程中,当$h_{1}= 1m$时,测力计示数$F_{1}= 3N$由此推断:金属棒的重心到A端距离$d= $ m;当$h_{2}= 2m$时,拉力$F_{1}总共做W_{2}= $ J.

答案：

(1)B
(2)0.72 7.6 解析:
(1)当金属棒没离开地面时,金属棒是在拉力作用下绕着 A 端被缓慢匀速提起,此时金属棒是杠杆,支点为 A,动力为测力计对金属棒的拉力,阻力为金属棒的重力,其中棒长 L,设金属棒的重心离 A 端距离为 d,如图: 根据杠杆的平衡条件可得 F₁L₁ = GL₂,且由数学知识可得 $\frac{L₁}{L₂}$ = $\frac{L}{d}$,所以 $\frac{F₁}{G}$ = $\frac{d}{L}$,这一过程中测力计对金属棒的拉力 F₁不变,且 F₁ ＜ G.金属棒没离开地面时,测力计对棒所做的功 W = F₁h,因 F₁ 不变,所以 W 和 h 成正比关系;当金属棒 AB 离开地面后,因竖直匀速提起金属棒,所以由二力平衡条件可知,拉力为 F₁' = G = 5 N,测力计对棒所做的功 W' = F₁'h,且此过程中 F₁'不变,故 W'和 h 也成正比关系,但 F₁' ＞ F₁,所以提升相同高度时拉力做功更多,即图线更陡.综上,B 图最能表现弹簧测力计对棒所做的功 W 与 B 端离开地面的高度 h 的关系,故应该选 B.
(2)当 h₁ = 1 m 时,此时金属棒 A 端还未脱离地面,测力计的示数 F₁为 3 N,由
(1)可知, $\frac{F₁}{G}$ = $\frac{d}{L}$,代入 F₁ = 3 N,G = 5 N,L = 1.2 m,解得 d = 0.72 m,即金属棒的重心到 A 端的距离 d 为 0.72 m.当 h₂ = 2 m 时,金属棒 AB 已经离开地面,未离开地面时,弹簧测力计示数 F₁为 3 N 且不变,弹簧测力计对棒做的功为 W₁ = F₁L = 3 N×1.2 m = 3.6 J.金属棒离开地面继续上升的高度为 h₂ = 2 m - 1.2 m = 0.8 m,离开地面后,弹簧测力计对棒所做的功为克服棒重力做的功为 W₂ = Gh₂ = 5 N×0.8 m = 4 J.故当 h₂ = 2 m 时,拉力 F 做的功为 W₈ₐₐ = W₁ + W₂ = 3.6 J + 4 J = 7.6 J.