《2025年学霸题中题九年级物理上册苏科版》

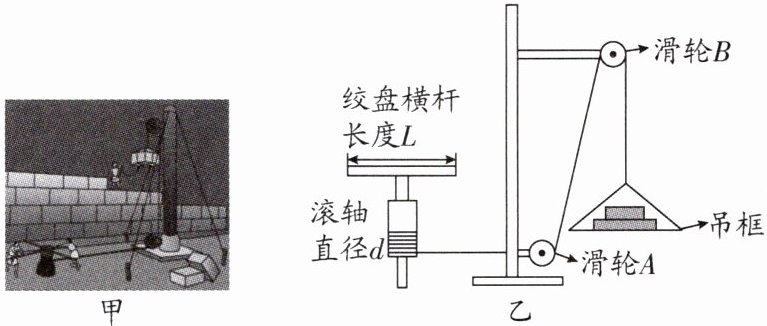
1. (2025·无锡锡北片区期中)如图甲所示是我国古人使用绞车和滑轮吊起石材时的模拟图,其简化结构图如图乙所示,绞盘横杆长度L与滚轴直径d之比为4∶1,已知每块大理石的重力为280 N,吊框的重力为100 N,不计绳重和机械间的所有摩擦,g取10 N/kg.

(1)绞车可以看作______(填“轮轴”或“斜面”)。
(2)一位工匠的最大推力为400 N,在某次工作中,该工匠匀速推动绞车提升大理石板10 m。
①在绳子最大拉力足够的情况下该工匠最多一次能够借助绞车吊起多少块大理板？
②此时绞车的机械效率为多少？(百分号前保留1位小数)
[答案]：1.
(1)轮轴
(2)①5块 ②93.3% 解析:
(1)通过转动绞盘使绳子缠绕滚轴,从而拉起物体,绞盘相当于轮,滚轴相当于轴,所以绞车可以看作轮轴.
(2)①一位工匠的最大推力为400 N,绞盘横杆长度L与滚轴直径d之比为4:1,则绳子的最大拉力$ F=\frac{F_{1}× \frac{1}{2}L}{\frac{1}{2}d}=4F_{1}=4× 400\ \text{N}=1600\ \text{N} $,每块大理石的重力为280 N,吊框的重力为100 N,则工匠最多一次能够借助绞车吊起大理石数量$ n=\frac{F-G_{\text{框}}}{G_{\text{石}}}=\frac{1600\ \text{N}-100\ \text{N}}{280\ \text{N}}\approx5 $块;②吊起5块大理石时绞车的机械效率$ \eta=\frac{W_{\text{有用}}}{W_{\text{总}}}×100\%=\frac{5G_{\text{石}}h}{(5G_{\text{石}}+G_{\text{框}})h}×100\%=\frac{5×280\ \text{N}}{5×280\ \text{N}+100\ \text{N}}×100\%\approx93.3\% $.

答案： 1.
(1)轮轴
(2)①5块 ②93.3% 解析:
(1)通过转动绞盘使绳子缠绕滚轴,从而拉起物体,绞盘相当于轮,滚轴相当于轴,所以绞车可以看作轮轴.
(2)①一位工匠的最大推力为400 N,绞盘横杆长度L与滚轴直径d之比为4:1,则绳子的最大拉力$ F=\frac{F_{1}× \frac{1}{2}L}{\frac{1}{2}d}=4F_{1}=4× 400\ \text{N}=1600\ \text{N} $,每块大理石的重力为280 N,吊框的重力为100 N,则工匠最多一次能够借助绞车吊起大理石数量$ n=\frac{F-G_{\text{框}}}{G_{\text{石}}}=\frac{1600\ \text{N}-100\ \text{N}}{280\ \text{N}}\approx5 $块;②吊起5块大理石时绞车的机械效率$ \eta=\frac{W_{\text{有用}}}{W_{\text{总}}}×100\%=\frac{5G_{\text{石}}h}{(5G_{\text{石}}+G_{\text{框}})h}×100\%=\frac{5×280\ \text{N}}{5×280\ \text{N}+100\ \text{N}}×100\%\approx93.3\% $.

2. 机械手臂是机器人技术领域中的自动化机械装置,能够接受指令,完成抓取、伸缩、旋转和升降等动作.某实验小组制作了如图甲所示的机械手臂模型,并安装在一辆小车上,其结构简图如图乙所示,工作时安装在小车上的底座可以在水平面内自由旋转,产柱和横臂可以在竖直面内自由旋转,手爪可以抓取不同方向、不同高度的物体.
(1)如图丙所示为手爪的示意图,拉动上方的细线,弯曲件AOBC可绕O点转动,弯曲件AOBC此时为______杠杆,同时拉动两根细线手爪就可夹住物体,利用C点产生的______力将物体举高.为防止手爪在夹物体时给物体造成伤害,可以增大C点处的______.
(2)如图丁所示,电控组件的质量为500 g,忽略小车、底座、产柱、横臂和手爪的重力,相关参数如图所示(单位：cm),当机械手臂产柱竖直、横臂水平没有抓取物块时,为防止小车轮子脱离地面,所加配重至少为______N.当此机械臂抓取正前方一个质量为200 g的金属块,将其举高20 cm,对金属块做功为______J,在加上最小配重后,在产柱竖直,横臂最终水平状态下,为防止在抓取过程中小车轮子脱离地面,抓取物体的最大重力为______N.在不增加器材的情况下,要想横臂最终保持水平位置并增加抓取物体的最大重力,可行的方法是：______.
(1)费力 摩擦 接触面积
(2)1.25 0.4 4.6875 将机械产柱向左侧转动

答案： 2.
(1)费力 摩擦 接触面积
(2)1.25 0.4 4.6875 将机械产柱向左侧转动
解析:
(1)由图丙知,弯曲件AOBC在绕O点转动时,阻力臂大于动力臂,故其属于费力杠杆.机械臂用手爪抓取物体时,利用手爪C点对物体的摩擦力,从而防止物体滑落,进而能将物体举高.在压力一定时,可以增大接触面积从而减小压强,所以为了防止手爪抓物体造成伤害,可以增大C点处的接触面积.
(2)由题意知,电控组件的质量为500 g,由$ G=mg $可得,电控组件受到的重力为$ G_{\text{件}}=m_{\text{件}}g=0.5\ \text{kg}×10\ \text{N/kg}=5\ \text{N} $;以左轮为支点,设配重为$ G_{\text{配}} $时,根据杠杆平衡条件可得$ G_{\text{件}}× l_{1}=G_{\text{配}}× l_{2} $,则$ 5\ \text{N}×5\ \text{cm}=G_{\text{配}}×20\ \text{cm} $,解得$ G_{\text{配}}=1.25\ \text{N} $,由此可知,为防止小车轮子脱离地面,所加配重至少为1.25 N.由$ G=mg $可得,200 g的金属块所受重力为$ G_{\text{金属块}}=m_{\text{金属块}}g=0.2\ \text{kg}×10\ \text{N/kg}=2\ \text{N} $,由$ W=Gh $可得,将该金属块举高20 cm的过程中,对金属块做功$ W=G_{\text{金属块}}h=2\ \text{N}×0.2\ \text{m}=0.4\ \text{J} $.以右轮为支点,设抓取的重物最大重力为$ G_{\text{物}} $,根据杠杆平衡条件可得$ G_{\text{件}}× l_{1}'=G_{\text{配}}× l_{2}'+G_{\text{物}}× l_{3} $,则$ 5\ \text{N}×20\ \text{cm}=1.25\ \text{N}×5\ \text{cm}+G_{\text{物}}×(25\ \text{cm}-5\ \text{cm}) $,解得$ G_{\text{物}}=4.6875\ \text{N} $.由题意知,在不增加器材的情况下,增加横臂最终抓取物体的最大重力,可将机械臂产柱向左转动,使重物重心向左移,从而增加抓取物体的最大重力.