《2025年学霸题中题九年级物理上册苏科版》

8.(2024·甘肃中考)将物体A、B置于如图所示的装置中,物体B恰好匀速下降,已知A重60 N,B重10 N,则A所受地面的摩擦力为20N;若对A施加一个水平向左的拉力F,刚好使A在原来的水平面上匀速向左运动,则拉力F大小为40N.(不计绳重、滑轮重及绳子与滑轮间的摩擦)

答案： 20　40　解析:如题图所示，动滑轮上有2段绳子，已知B重10N，物体B恰好匀速下降，则A匀速向右运动，说明物体A处于平衡状态，则A所受地面的摩擦力与动滑轮的钩子拉A的力是一对平衡力，即$f=F_{拉}=2G_{B}=2×10N=20N$；若对A施加一个水平向左的拉力F，则物体A受到三个力的作用：水平向左的拉力F，水平向右的拉力$F_{拉}$，水平向右的摩擦力$f'=20N$，水平向左的拉力F刚好使A匀速向左运动，则拉力$F=f+F_{拉}=f'+2G_{B}=20N+2×10N=40N$。

9. 如图所示,某工人站在地面上使用由三个滑轮组成的滑轮组提升重物,请画出最省力的绕绳方法.

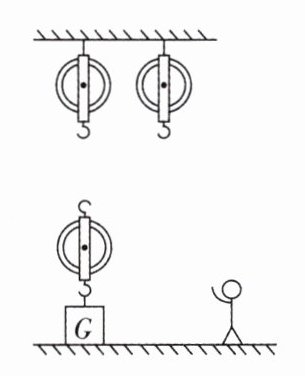
答案：
如图所示　　　　　　　　 　解析:由于图中只有一个动滑轮，承担物重的绳子段数最多为3段，此时最省力。

10. 如图甲所示,某同学用两个滑轮组成的滑轮组,在同一种绕绳方式下匀速提升不同质量的重物,得到了多组竖直作用在绳子自由端的拉力$F与重物所受重力G$的大小关系,并绘制出如图乙所示的图像,不计绳重与摩擦.则:
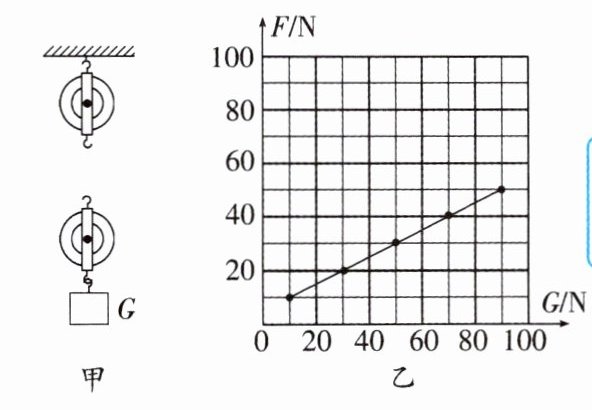
(1)根据图像计算动滑轮重力$G_{\text{动}}$= ______N.
(2)在图甲中画出该同学的绕绳方法.

答案：

(1)10　
(2)见解析图　　解析:
(1)如题图所示有两个滑轮组成滑轮组，一共有两种绕绳方式，绳子段数取$n=2$或$n=3$。　第一种绳子段数$n=2$，取乙图$G_{1}=30N$，$F_{1}=20N$；$G_{2}=50N$，$F_{2}=30N$；有$F_{1}=\frac {1}{2}(G_{1}+G_{动})$，代入数值，得$G_{动}=10N$；将$G_{2}=50N$，$G_{动}=10N$代入$F'_{2}=\frac {1}{2}(G_{2}+G_{动})=\frac {1}{2}×(50N+10N)=30N$，与乙图中$F_{2}=30N$相等，故这种情况符合题意，动滑轮重力为10N。　第二种绳子段数$n=3$，取乙图$G_{1}=30N$，$F_{1}=20N$；$G_{2}=50N$，$F_{2}=30N$；有$F_{1}=\frac {1}{3}(G_{1}+G'_{动})$，代入数值，得$G'_{动}=30N$，将$G_{2}=50N$，$G'_{动}=30N$代入$F''_{2}=\frac {1}{3}(G_{2}+G'_{动})=\frac {1}{3}×(50N+30N)=\frac {80}{3}N$，与乙图中$F_{2}=30N$不相等，故这种情况不符合题意。　　
(2)由
(1)可得该同学的绕线方法，如图所示:　　　　　　　　　　

11. 小明想利用滑轮设计一款锻炼拉力的健身器材,能满足拉力大小200~400 N的健身者的使用需求.设计要求如下:竖直向下匀速拉动拉环时,配重匀速向上提升;拉环竖直向下移动0.5 m时,配重竖直向上移动的距离不超过1.5 m;配重质量可根据健身者需求,在5~20 kg范围内任选(滑轮、绳子、拉环的质量和摩擦均不计,绳子长度足够长,滑轮数量不限,$g$取10 N/kg).图1为小明设计的方案,请你在图2框中设计出另一种方案.

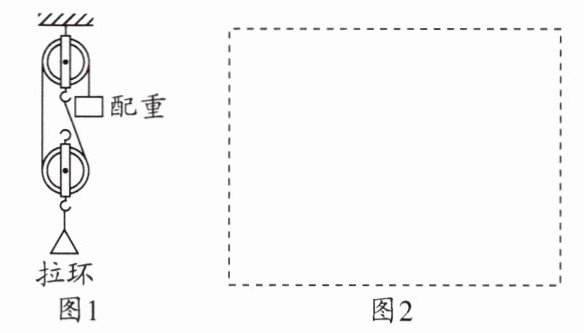
答案：
如图所示　　　 　　 　　 解析:由题意可知，配重的质量可选范围为5~20kg，则配重重力范围为50~200N，小于健身者的拉力范围200~400N，所以设计滑轮组时，配重悬挂在绳自由端，拉环挂在动滑轮的挂钩上。拉环竖直向下移动0.5m时，配重竖直向上移动的距离不超过1.5m，说明滑轮组中，承重的绳子段数$n≤3$。当$n=2$时，拉力200~400N的健身者，选择的配重应为100~200N，对应的配重质量为10~20kg，在选择范围内，符合题意。此时的滑轮组由1个动滑轮和1个定滑轮组成，除图1的连接方式外，还可采用动滑轮单独悬挂的方式，如图(a)；当$n=3$时，拉力200~400N的健身者，选择的配重应为67~133N，对应的配重质量为6.7~13.3kg，在选择范围内，符合题意。此时的滑轮组由1个动滑轮和2个定滑轮组成，连接方式可以如图(b)与图(c)所示。

12. 如图所示,用起重机打捞水中的物体,物体的质量为1500 kg,体积为600 dm^3,起重机(含滑轮组)自重和摩擦均忽略不计,$g$取10 N/kg,求:
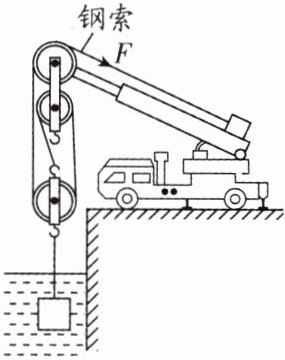
(1)物体完全在水中被匀速提升时,起重机钢索上的拉力$F$多大?
(2)如果起重机的钢索能承受的最大拉力为4500 N,当物体被匀速提升,露出水面的体积多大时会被拉断?

答案：
(1)3000N　
(2)450dm³ 　解析:
(1)物体的重力：　$G=mg=1500kg×10N/kg=15000N$，　物体浸没在水中受的浮力：$F_{浮}=ρ_{水}V_{排}g=ρ_{水}Vg=1.0×10^{3}kg/m^{3}×600×10^{-3}m^{3}×10N/kg=6000N$；　滑轮组对物体的拉力：　$F_{拉}=G - F_{浮}=15000N - 6000N=9000N$，　因为起重机(含滑轮组)自重和摩擦均忽略不计，$n=3$，　所以起重机钢索上的拉力：　$F=\frac {1}{3}F_{拉}=\frac {1}{3}×9000N=3000N$。　
(2)由题知，滑轮组钢索能承受的最大拉力为4500N，即$F_{最大}=4500N$，起重机(含滑轮组)自重和摩擦均忽略不计，钢索上的最大拉力$F_{最大}=\frac {1}{3}F'_{拉}$，　所以，滑轮组对物体的最大拉力为：　$F'_{拉}=3F_{最大}=3×4500N=13500N$，对水中的物体来说，根据力的平衡条件有：$G=F'_{浮}+F'_{拉}$，所以此时物体受到的浮力：　$F'_{浮}=G - F'_{拉}=15000N - 13500N=1500N$，　因为$F'_{浮}=ρ_{水}V'_{排}g$，所以，此时物体排开水的体积：　$V'_{排}=\frac {F'_{浮}}{ρ_{水}g}=\frac {1500N}{1×10^{3}kg/m^{3}×10N/kg}=0.15m^{3}$；　此时物体露出水面的体积为：　$V_{露}=V - V'_{排}=0.6m^{3}-0.15m^{3}=0.45m^{3}=450dm^{3}$。