《2025年5年中考3年模拟物理》

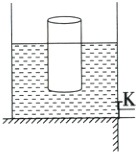
12.[2024云南]一质量为900 g、底面积为100 cm²、高为12 cm的不吸水圆柱体放在盛有4.2 kg水的薄壁(厚度不计)柱形容器内,容器底面积为300 cm²,如图所示。打开阀门K,放出3 kg的水后关闭阀门(ρ水 = 1.0×10³ kg/m³,g取10 N/kg)。下列说法正确的是　　　　　　　　　　　[多选](　　　)

A.圆柱体的密度为0.75×10³ kg/m³
B.放水前水面距容器底部的高度为14 cm
C.放水后水对容器底部的压力为21 N
D.放水后水对容器底部的压强为600 Pa

答案： AD 解析：圆柱体的密度$\rho=\frac{m}{V}=\frac{0.9\ kg}{1\times10^{-2}\ m^{2}\times0.12\ m}=0.75\times10^{3}\ kg/m^{3}$，A正确。放水前圆柱体处于漂浮状态，$F_{浮}=G_{柱}=G_{排}$，则$V_{排}=\frac{m}{\rho_{水}}=\frac{0.9\ kg}{1.0\times10^{3}\ kg/m^{3}}=9\times10^{-4}\ m^{3}=900\ cm^{3}$，放水前容器内水的体积$V=\frac{m_{水}}{\rho_{水}}=\frac{4.2\ kg}{1.0\times10^{3}\ kg/m^{3}}=4.2\times10^{-3}\ m^{3}=4200\ cm^{3}$，放水前水面距容器底部的高度$h=\frac{V_{排}+V}{S_{容}}=\frac{900\ cm^{3}+4200\ cm^{3}}{300\ cm^{2}}=17\ cm$，B错误。$\rho＜\rho_{水}$，柱形容器的底面积是圆柱体底面积的3倍，圆柱体在该容器中刚好漂浮所需要水的最小质量$m_{min}=2m_{排水}=2m = 2\times900\ g = 1.8\ kg$，放水后容器内剩余水的质量$m' = 1.2\ kg＜m_{min}$，所以放水后圆柱体无法漂浮。放水后水面的高度$h'=\frac{m'}{\rho_{水}(S_{容}-S_{柱})}=\frac{1.2\ kg}{1.0\times10^{3}\ kg/m^{3}\times(0.03\ m^{2}-0.01\ m^{2})}=0.06\ m$，放水后水对容器底部的压强$p=\rho_{水}gh'=1.0\times10^{3}\ kg/m^{3}\times10\ N/kg\times0.06\ m = 600\ Pa$，水对容器底部的压力$F = pS_{容}=600\ Pa\times0.03\ m^{2}=18\ N$，C错误，D正确。故选AD。

13.[2024广西]一个不吸水的实心圆柱体Q,底面积为0.01 m²,高为0.3 m,密度为0.5×10³ kg/m³。如图甲所示,现将Q放在容器中,缓慢往容器中注水(水的密度为1×10³ kg/m³,g取10 N/kg),求:
(1)圆柱体Q的质量;
(2)当注入水的深度为0.1 m时(此时Q未漂浮),Q受到的浮力;
(3)广西夏季雨水充沛,每逢暴雨,河水水位快速上涨,为了监测河水水位,某项目小组设计了“智能水位报警器”,如图乙所示。其由A、B两部分组成,A模拟控制器,B模拟河道。其中A内部高度为0.7 m,顶部固定着压力传感器,当压力达到某一数值时,报警器会自动报警。在某次注水测试中,当注水到某一深度时,Q开始漂浮,随着注入水的深度增加,Q最终会与传感器接触,当Q露出水面长度为0.1 m时,报警器恰好开始报警。请通过计算,分析从开始注水到报警器报警的过程,并在图丙中作出此过程Q底部受到水的压强p随注入水的深度h变化的关系图线。

答案：

(1)$1.5\ kg$
(2)$10\ N$
(3)见解析
解析：
(1)Q的体积$V_{Q}=S_{Q}h_{Q}=0.01\ m^{2}\times0.3\ m = 3\times10^{-3}\ m^{3}$，Q的质量$m_{Q}=\rho_{Q}V_{Q}=0.5\times10^{3}\ kg/m^{3}\times3\times10^{-3}\ m^{3}=1.5\ kg$。
(2)注水深度为$0.1\ m$时，Q排开水的体积为$V_{排}=S_{Q}h_{浸1}=0.01\ m^{2}\times0.1\ m = 1\times10^{-3}\ m^{3}$，Q受到的浮力$F_{浮}=\rho_{水}gV_{排}=1\times10^{3}\ kg/m^{3}\times10\ N/kg\times1\times10^{-3}\ m^{3}=10\ N$。
(3)①设注入水的深度为$h_{1}$时，Q恰好开始漂浮，此时Q受到的浮力等于重力，有$G_{Q}=F_{浮1}=\rho_{水}gV_{排1}$即$m_{Q}g=\rho_{水}gS_{Q}h_{1}$，解得$h_{1}=\frac{m_{Q}}{\rho_{水}S_{Q}}=\frac{1.5\ kg}{1\times10^{3}\ kg/m^{3}\times0.01\ m^{2}}=0.15\ m$，此时，Q底部受到的水的压强$p_{1}=\rho_{水}gh_{1}=1\times10^{3}\ kg/m^{3}\times10\ N/kg\times0.15\ m = 1.5\times10^{3}\ Pa$，故注入水的深度小于$0.15\ m$的过程中，Q底部受到水的压强与注入水的深度成正比，故该过程$p - h$图线是一条倾斜线段。
②继续注水，直到Q的顶端恰好与传感器接触，设注入水的深度为$h_{2}$，有$h_{2}=H-(h_{Q}-h_{1})=0.7\ m-(0.3\ m - 0.15\ m)=0.55\ m$，从Q恰好开始漂浮到顶部恰好接触传感器的过程中，Q浸入水中的深度不变，故Q底部受到水的压强不变，得$p_{2}=p_{1}=1.5\times10^{3}\ Pa$，故注入水的深度从$0.15\ m$到$0.55\ m$的过程中，$p - h$图线是一条水平线段。
③继续注水，Q被传感器阻挡，不再上升，当Q露出水面$0.1\ m$时，注入水的深度$h_{3}=H - h_{露}=0.7\ m - 0.1\ m = 0.6\ m$。此时，Q浸入水中深度$h_{浸2}=h_{Q}-h_{露}=0.3\ m - 0.1\ m = 0.2\ m$，Q底部受到水的压强$p_{3}=\rho_{水}gh_{浸2}=1\times10^{3}\ kg/m^{3}\times10\ N/kg\times0.2\ m = 2\times10^{3}\ Pa$。故注入水的深度从$0.55\ m$到$0.6\ m$的过程中，Q浸入水中深度为$h_{浸}=0.3\ m-(0.7\ m - h)=h - 0.4\ m$，Q底部受到水的压强$p=\rho_{水}gh_{浸}=\rho_{水}g(h - 0.4\ m)$，故此过程$p - h$图线是一条倾斜线段。
综合①②③，可作出$p - h$图线如图所示。