《2025年5年中考3年模拟物理》

8.[2024四川泸州]中国长征18号核潜艇引领中国核潜艇新高度。在进行战备训练时,下列对该潜艇的说法中正确的是　　　　　　(　　　)
A.通过改变排开水的体积来实现上浮与下沉
B.在水面下匀速下潜过程中,受到的浮力增大
C.从长江潜行进入东海时,需要向水舱内注水
D.从长江潜行进入东海时,受到的浮力会变小

答案： C

9.[2024湖南长沙模拟]关于轮船下列说法不正确的是　　　　　　　　　　　　　　　(　　　)
A.钢铁制作成轮船,是采用“空心技术”,增大了排开液体的体积,增大了浮力
B.在海面上匀速航行时,所受浮力等于轮船的重力
C.轮船从河里驶入海里,它受到的浮力不变,它将会上浮一些
D.向停靠在港口的轮船加装货物时,轮船始终处于漂浮状态，这个过程中浮力大小不变

答案： D

10.[2024安徽滁州一模]小明利用一根一端开口的重为2 N、长为L的玻璃管和橡皮塞制作了密度计,但发现自制的密度计平躺在水面且有$\frac{4}{5}$的体积露出水面,如图甲所示。他查阅资料得知,在物理学中,浮力的作用点叫浮心。由阿基米德原理可知,浮力的大小等于物体排开的液体所受的重力大小,因此浮心的位置就是那部分被排开的液体的重心位置。已知水的密度为1.0×10³ kg/m³。忽略橡皮塞的质量及体积。

(1)在图甲中用“·”标出浮心,并画出密度计受到的浮力F浮的示意图。
(2)为使自制的密度计竖立在水中,小明在玻璃管内装入密度较大的液体,当密度计竖立在水中时,密度计的重心与浮心重合,如图乙所示。测得此时密度计浸在水中的长度为0.4L,计算此时密度计所受浮力的大小。
(3)如图丙所示,将自制的密度计放入待测液体中,静止时,密度计浸在待测液体中的长度为0.5L,求待测液体的密度。

答案：

(1)见解析图
(2)$4\ N$
(3)$0.8\times10^{3}\ kg/m^{3}$
解析：
(1)密度计的浮心在浸入水中部分的几何中心，且浮力等于重力(2 N)，方向竖直向上，如图所示。
　　　　　　　
(2)由题意可知，当自制密度计(玻璃管和橡皮塞)平躺在水面且有$\frac{4}{5}$的体积露出水面时，浮力等于其重力，即$F_{浮}=\frac{1}{5}\rho_{水}V_{密度计}g = G = 2\ N$，玻璃管内装入密度较大的液体后，密度计竖立在水中时，浸在水中的长度为$0.4L$，此时排开水的体积$V_{排水}=\frac{0.4L}{L}\times V_{密度计}=\frac{2}{5}V_{密度计}$，根据$F_{浮}=\rho_{液}gV_{排}$可知，此时的浮力$F_{浮1}=\frac{2}{5}\rho_{水}V_{密度计}g = 2F_{浮}=2\times2\ N = 4\ N$。
(3)将自制的密度计放入待测液体中后，密度计排开液体的体积$V_{排液}=\frac{0.5L}{L}\times V_{密度计}=\frac{1}{2}V_{密度计}$，根据$F_{浮}=\rho_{液}gV_{排}$可知，此时的浮力$F_{浮2}=\frac{1}{2}\rho_{液}V_{密度计}g$，该自制密度计仍处于漂浮状态，受到的浮力仍等于密度计的重力$G'$，则$F_{浮2}=G'=F_{浮1}$，即$\frac{1}{2}\rho_{液}V_{密度计}g=\frac{2}{5}\rho_{水}V_{密度计}g$，待测液体的密度$\rho_{液}=\frac{4}{5}\rho_{水}=\frac{4}{5}\times1.0\times10^{3}\ kg/m^{3}=0.8\times10^{3}\ kg/m^{3}$。

11.[2024四川达州]如图甲所示,悬挂在弹簧测力计下的实心圆柱体A浸没在水中,将其缓慢拉出水面(忽略物体带出的水),弹簧测力计的示数F与圆柱体A上升的高度h之间的变化图像如图乙所示。然后将体积为2 000 cm³的实心物体B用细线和A连接在一起,如图丙所示放入水中,A、B刚好悬浮。细线的重力和体积忽略不计,ρ水=1.0×10³ kg/m³,g取10 N/kg,下列说法正确的是　　　　　　　　　　(　　　)

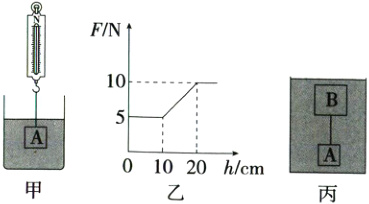
A.A浸没在水中所受浮力为10 N
B.A的底面积为50 cm²
C.B的重力为20 N
D.B的密度为0.75×10³ kg/m³

答案： D 解析：由图乙可知，圆柱体A上升高度为0~10 cm时，弹簧测力计的示数不变，说明圆柱体A未露出水面，此时弹簧测力计的示数$F_{示}=5\ N$；圆柱体A上升高度超过20 cm时，弹簧测力计的示数不变，说明圆柱体A已完全露出水面，此时弹簧测力计的示数$F_{示}' = 10\ N$，则圆柱体A的重力$G_{A}=F_{示}' = 10\ N$，圆柱体A浸没在水中时受到的浮力$F_{浮}=G_{A}-F_{示}=10\ N - 5\ N = 5\ N$，故A错误；由$F_{浮}=\rho_{液}gV_{排}$可得，圆柱体A的体积$V_{A}=V_{排}=\frac{F_{浮}}{\rho_{水}g}=\frac{5\ N}{1.0\times10^{3}\ kg/m^{3}\times10\ N/kg}=5\times10^{-4}\ m^{3}$，假设从水中拉出圆柱体A过程中，容器中的水面高度不变，则圆柱体A的底面积$S_{A}=\frac{V_{A}}{\Delta h}=\frac{5\times10^{-4}\ m^{3}}{0.2\ m - 0.1\ m}=5\times10^{-3}\ m^{2}=50\ cm^{2}$，实际从水中拉出圆柱体A的同时，容器中的水面在下降，圆柱体A从刚露出水面到离开水面上升的高度小于A的高，故B错误；体积为$2000\ cm^{3}$的实心物体B和A在水中悬浮，则A、B的总重力$G_{总}=F_{浮}'=\rho_{水}gV_{排}'=\rho_{水}g(V_{A}+V_{B})=1.0\times10^{3}\ kg/m^{3}\times10\ N/kg\times(5\times10^{-4}\ m^{3}+2\times10^{-3}\ m^{3})=25\ N$，则B的重力$G_{B}=G_{总}-G_{A}=25\ N - 10\ N = 15\ N$，故C错误；B的密度$\rho_{B}=\frac{m_{B}}{V_{B}}=\frac{G_{B}}{gV_{B}}=\frac{15\ N}{10\ N/kg\times2\times10^{-3}\ m^{3}}=0.75\times10^{3}\ kg/m^{3}$，故D正确。