《2025年5年中考3年模拟物理》

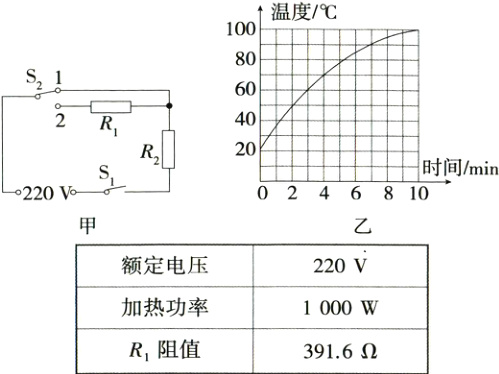
6.[2024江苏扬州二模]如图甲是电水壶简化电路图，R₁和R₂为发热电阻，S₁为总开关，S₂为温控开关，有1、2两个触点，控制电水壶的“加热”和“保温”两挡，表中数据为电水壶的部分工作参数。
　(1)电阻R₂的阻值为多少？
　(2)电水壶的保温功率为多少？
　(3)电水壶中装进1kg水进行加热，用温度计测量水温，得到水温随时间变化的图像如图乙，则第4min至第10min时间段内水吸收的热量是多少？这段时间内电水壶的加热效率η是多少？[c水 = 4.2×10³J/(kg·℃)]
　

答案：
(1)48.4 Ω
(2)110 W
(3)1.26×10⁵ J 35%
解析:
(1)由电路图可知，S₁闭合，S₂接1时，只有电阻R₂接入电路中，此时电路的总电阻最小，由电功率的推导式可知，此时电路的总功率最大，所以电水壶处于加热挡。由表可知加热挡时的电功率为1 000 W，所以可得R₂的阻值R₂ = $\frac{U^{2}}{P}$ = $\frac{(220\ V)^{2}}{1 000\ W}$ = 48.4 Ω。
(2)S₁闭合，S₂接2时，R₁、R₂串联，电水壶处于保温挡，串联的总电阻R = R₁ + R₂ = 391.6 Ω + 48.4 Ω = 440 Ω，电水壶的保温功率P保 = $\frac{U^{2}}{R}$ = $\frac{(220\ V)^{2}}{440\ Ω}$ = 110 W。
(3)由图像可知第4 min至第10 min时间段内水升高的温度为ΔT = 100 ℃ - 70 ℃ = 30 ℃，则该段时间内水吸收的热量Q吸 = c水mΔT = 4.2×10³ J/(kg·℃)×1 kg×30 ℃ = 1.26×10⁵ J，烧水过程中电水壶处于加热挡，功率为1 000 W，则该段时间内电水壶消耗的电能W = Pt = 1 000 W×(10 - 4)×60 s = 3.6×10⁵ J，则电水壶的加热效率η = $\frac{Q_{吸}}{W}$ = $\frac{1.26×10^{5}\ J}{3.6×10^{5}\ J}$ = 35%。

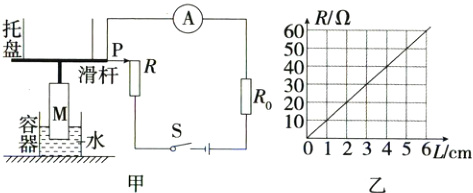
7.[2024四川南充]科创小组设计利用电流表测量质量的装置如图。现截取适当长度的电阻片R(它的阻值随长度L的变化图像如图乙)作为滑动变阻器接入电路，如图甲所示。如图甲中，电源电压6V恒定不变，电流表量程为0~0.6A。当滑片P在最下端时，电流表示数为0.6A。装置中托盘与圆柱形实心塑料浮筒M通过硬质绝缘细杆固定连接，整体漂浮在装有足够深水的柱形薄壁容器中，且只能竖直移动。托盘的质量为0.27kg；M高22cm，底面积为300cm²，质量为0.33kg；容器的底面积为400cm²。托盘通过滑杆带动滑片P上下移动。托盘中未放物体时，调节水量，使滑片P正好位于R最上端。托盘中放入物体A时，M刚好浸没，滑片P正好位于R最下端(g取10N/kg、ρ水 = 1.0×10³kg/m³、不计滑片、滑杆、细杆的质量，忽略摩擦阻力，工作中水不溢出)。求：
　(1)R₀的阻值；
　(2)物体A的质量；
　(3)托盘中未放物体时，电流表的示数。
　

答案：
(1)10 Ω
(2)6 kg
(3)0.1 A
解析:
(1)当滑片P位于R最下端时，R = 0，I = 0.6 A，R₀ = $\frac{U}{I}$ = $\frac{6\ V}{0.6\ A}$ = 10 Ω。
(2)当托盘中未放入物体时，F浮1 = G总1 = (m筒 + m盘)g = (0.33 kg + 0.27 kg)×10 N/kg = 6 N，当托盘中放入A物体时，M筒刚好浸没，则M筒浸入的深度为h筒 = 22 cm，V排2 = S筒h筒 = 300 cm²×22 cm = 6 600 cm³ = 6.6×10⁻³ m³，F浮2 = ρ水gV排2 = 1.0×10³ kg/m³×10 N/kg×6.6×10⁻³ m³ = 66 N，Gₐ = F浮2 - F浮1 = 66 N - 6 N = 60 N，mₐ = $\frac{G_{A}}{g}$ = $\frac{60\ N}{10\ N/kg}$ = 6 kg。
(3)当托盘中未放入物体时，排开水的体积为V排1 = $\frac{F_{浮1}}{\rho_{水}g}$ = $\frac{6\ N}{1.0×10^{3}\ kg/m^{3}×10\ N/kg}$ = 6×10⁻⁴ m³ = 6×10² cm³，M浸入的深度为h₀ = $\frac{V_{排1}}{S_{筒}}$ = $\frac{6×10^{2}\ cm^{3}}{300\ cm^{2}}$ = 2 cm，设托盘中放入A物体，M下降的高度为h₁，液面上升的高度为h₂，由题意可得(S容 - S筒)h₂ = S筒h₁，代值得(400 cm² - 300 cm²)h₂ = 300 cm²·h₁，即h₂ = 3h₁，又因为h₀ + h₁ + h₂ = h筒，把h₂ = 3h₁代入得h₀ + h₁ + 3h₁ = h筒，即h₁ = $\frac{h_{筒}-h_{0}}{4}$，代值得h₁ = $\frac{22\ cm - 2\ cm}{4}$ = 5 cm，由图乙可知，当L = h₁ = 5 cm时，R = 50 Ω，此时电路中电流I' = $\frac{U}{R + R_{0}}$ = $\frac{6\ V}{50\ Ω + 10\ Ω}$ = 0.1 A，即当托盘中不放物体时，电流表示数为0.1 A。