《2025年课堂点睛八年级数学下册人教版安徽专版》

14. 如图,在Rt△ABC中,∠BAC=90°,AB=9,AC=6,点D为AC的中点,AF⊥BD于点E.
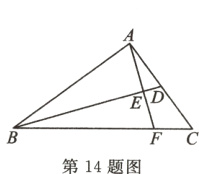
(1)AE的长为________; (2)$\frac{CF}{BF}$的值为________.
　

答案：
(1)$\frac{9\sqrt{10}}{10}$
(2)$\frac{2}{9}$

15. 计算:
(1)在Rt△ABC中,∠C=90°,AC=16,BC=12,求AB的长.(4分)
(2)在Rt△ABC中,∠C=90°,AB=41,BC=40,求AC的长.(4分)

答案：
(1)解：根据勾股定理，得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{16^{2}+12^{2}}=20$。
(2)根据勾股定理，得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{41^{2}-40^{2}}=9$。

16. 如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17,求CD的长及$S_{\triangle ABC}$.
　

答案： 解：$\because BD^{2}+AD^{2}=6^{2}+8^{2}=100$，$AB^{2}=10^{2}=100$，$\therefore AD^{2}+BD^{2}=AB^{2}$，$\therefore \triangle ADB$为直角三角形，$\therefore \angle ADB = 90^{\circ}$，$\therefore \angle ADC = 90^{\circ}$。$\therefore CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{17^{2}-8^{2}}=15$。$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times(6 + 15)\times8 = 84$。

17. “中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过70km/h. 如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?（参考数据转换:1m/s=3.6km/h）

答案： 解：在$Rt\triangle ABC$中，$AC = 30m$，$AB = 50m$；根据勾股定理可得：$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{50^{2}-30^{2}}=40(m)$，$\therefore$小汽车的速度为$v=\frac{40}{2}=20(m/s)=72(km/h)$。$\because 72km/h＞70km/h$，$\therefore$这辆小汽车超速行驶。答：这辆小汽车超速了。