《2025年课堂点睛八年级数学下册人教版安徽专版》

8. 如图,在Rt△ABC中,∠ACB = 90°,AD为中线,E为AD的中点,DF//CE交BE于点F.若AC = 8,BC = 12,则DF的长为 （ ）

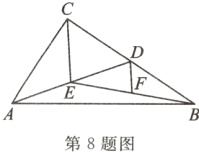
A. 2
B. 4
C. 3
D. 2.5

答案： D

9. 如图,平行四边形ABCD中,对角线AC、BD相交于O,过点O作OE⊥AC交AD于点E,若AE = 4,DE = 3,AB = 5,则AC的长为 （ ）

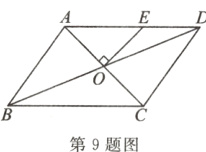
A. 3$\sqrt{2}$
B. 4$\sqrt{2}$
C. 5$\sqrt{2}$
D. $\frac{5\sqrt{2}}{2}$

答案： B

10. 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE = AE,则边BC的长为 （ ）

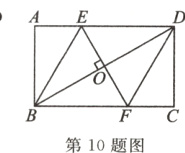
A. 2$\sqrt{3}$
B. 3$\sqrt{3}$
C. $\frac{9}{2}\sqrt{3}$
D. 6$\sqrt{3}$

答案： B

11. 如图,在□ABCD中,BD是对角线,E,F是对角线上的两点,要使四边形AFCE是平行四边形,还需添加一个条件(只需添加一个)是____________________.

答案： BF = DE(答案不唯一)

12. 如图是北京第24届国际数学家大会会标,它由4个全等的直角三角形拼合而成,若图中大、小正方形的面积分别为13和1,则直角三角形的较长直角边长为______.

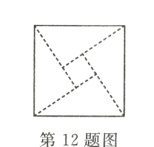
答案： 3

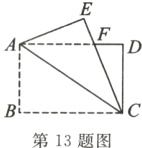
13. 如图,在矩形纸片ABCD中,AB = 4,BC = 6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长为________.

答案： $\frac{5}{3}$

14. 如图,在△ABC中,∠C = 90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE = AD,BF = BD,连接EF.
(1)∠EDF = ______;
(2)若DE = EF = $\sqrt{2}$,则线段AB的长为______.

答案：
(1)$45^{\circ}$
(2)$2\sqrt{5}$

15. 计算：
(1)$\sqrt{48}+\frac{1}{5}\sqrt{75}-3\sqrt{\frac{1}{3}}$;(4分)
(2)(2 - $\sqrt{3}$)²+($\sqrt{27}-\sqrt{12}$)÷$\sqrt{3}$.(4分)

答案：
(1)解：原式$=4\sqrt{3}+\frac{1}{5}\times5\sqrt{3}-\sqrt{3}=4\sqrt{3}$。
(2)解：原式$=4 - 4\sqrt{3}+3+(3 - 2)=8 - 4\sqrt{3}$。