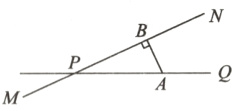
19. 如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,PA>100m,点A到公路MN的距离AB为80m,现有一卡车从点P出发,在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间有多长.

答案:
解:如图 ,设卡车开到C处时学校刚好开始受到噪音的影响,行驶到D处时结束了噪声的影响,连接AC,AD,则有$CA = DA = 100m$。在$Rt\triangle ABC$中,$CB=\sqrt{100^{2}-80^{2}}=60(m),\therefore CD = 2CB = 120m$。则该学校受影响的时间为$120\div5 = 24(s)$。答:该学校受影响的时间为24s。
,设卡车开到C处时学校刚好开始受到噪音的影响,行驶到D处时结束了噪声的影响,连接AC,AD,则有$CA = DA = 100m$。在$Rt\triangle ABC$中,$CB=\sqrt{100^{2}-80^{2}}=60(m),\therefore CD = 2CB = 120m$。则该学校受影响的时间为$120\div5 = 24(s)$。答:该学校受影响的时间为24s。
解:如图
 ,设卡车开到C处时学校刚好开始受到噪音的影响,行驶到D处时结束了噪声的影响,连接AC,AD,则有$CA = DA = 100m$。在$Rt\triangle ABC$中,$CB=\sqrt{100^{2}-80^{2}}=60(m),\therefore CD = 2CB = 120m$。则该学校受影响的时间为$120\div5 = 24(s)$。答:该学校受影响的时间为24s。
,设卡车开到C处时学校刚好开始受到噪音的影响,行驶到D处时结束了噪声的影响,连接AC,AD,则有$CA = DA = 100m$。在$Rt\triangle ABC$中,$CB=\sqrt{100^{2}-80^{2}}=60(m),\therefore CD = 2CB = 120m$。则该学校受影响的时间为$120\div5 = 24(s)$。答:该学校受影响的时间为24s。 20. (1)用“>”“<”或“=”填空:(4分)
$\frac{1}{2}+\frac{1}{3}$______2$\sqrt{\frac{1}{2}\times\frac{1}{3}}$;6 + 3______2$\sqrt{6\times3}$;
1+$\frac{1}{5}$______2$\sqrt{1\times\frac{1}{5}}$;7 + 7______2$\sqrt{7\times7}$;
(2)由(1)中各式猜想a + b与2$\sqrt{ab}$(a≥0,b≥0)的大小关系,并说明理由;(3分)
(3)请利用上述结论解决下面的问题:
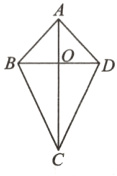
某同学在做一个面积为1800cm²,对角线相互垂直的四边形风筝(如图)时,用来做对角线的竹条至少要多少厘米?(3分)
$\frac{1}{2}+\frac{1}{3}$______2$\sqrt{\frac{1}{2}\times\frac{1}{3}}$;6 + 3______2$\sqrt{6\times3}$;
1+$\frac{1}{5}$______2$\sqrt{1\times\frac{1}{5}}$;7 + 7______2$\sqrt{7\times7}$;
(2)由(1)中各式猜想a + b与2$\sqrt{ab}$(a≥0,b≥0)的大小关系,并说明理由;(3分)
(3)请利用上述结论解决下面的问题:
某同学在做一个面积为1800cm²,对角线相互垂直的四边形风筝(如图)时,用来做对角线的竹条至少要多少厘米?(3分)

答案:
(1)$\gt$ $\gt$ $\gt$ $=$
(2)解:猜想$a + b\geqslant2\sqrt{ab}(a\geqslant0,b\geqslant0)$。理由如下:$\because a + b - 2\sqrt{ab}=(\sqrt{a})^{2}+(\sqrt{b})^{2}-2\sqrt{ab}=(\sqrt{a}-\sqrt{b})^{2}\geqslant0,\therefore a + b\geqslant2\sqrt{ab}$。
(3)设对角线的长分别是$a$cm,$b$cm,则$\frac{1}{2}ab = 1800,\therefore ab = 3600.\because a + b\geqslant2\sqrt{ab}=120,\therefore$用来做对角线的竹条至少要120cm。
(1)$\gt$ $\gt$ $\gt$ $=$
(2)解:猜想$a + b\geqslant2\sqrt{ab}(a\geqslant0,b\geqslant0)$。理由如下:$\because a + b - 2\sqrt{ab}=(\sqrt{a})^{2}+(\sqrt{b})^{2}-2\sqrt{ab}=(\sqrt{a}-\sqrt{b})^{2}\geqslant0,\therefore a + b\geqslant2\sqrt{ab}$。
(3)设对角线的长分别是$a$cm,$b$cm,则$\frac{1}{2}ab = 1800,\therefore ab = 3600.\because a + b\geqslant2\sqrt{ab}=120,\therefore$用来做对角线的竹条至少要120cm。
查看更多完整答案,请扫码查看


