七(本题满分12分)
22. 如图,在△ABC中,点D,E分别为BC,AC边上的中点,BE = 2DE,过点A作AF//BE交DE延长线于点F.
(1)求证:四边形ABEF为菱形;(6分)
(2)若∠ABE = 45°,AB = 4,求四边形ABDF的面积.(6分)

22. 如图,在△ABC中,点D,E分别为BC,AC边上的中点,BE = 2DE,过点A作AF//BE交DE延长线于点F.
(1)求证:四边形ABEF为菱形;(6分)
(2)若∠ABE = 45°,AB = 4,求四边形ABDF的面积.(6分)

答案:
(1)证明:
∵点D,E分别为BC,AC边上的中点,
∴DE是△ABC的中位线,
∴DE//AB,AB = 2DE.
∵EF//AB,AF//BE,
∴四边形ABEF是平行四边形.
∵BE = 2DE,
∴AB = BE,
∴四边形ABEF为菱形.
(2)解:如图 过E作EG⊥AB于G,由
过E作EG⊥AB于G,由
(1)可知,DE//AB,AB = 2DE,四边形ABEF为菱形,又
∵AB = 4,
∴DE = 2,BE = EF = AB = 4,
∴DF = DE + EF = 6. 在Rt△EBG中,∠ABE = 45°,
∴△EBG是等腰直角三角形,
∴EG = √2/2BE = 2√2,
∴S四边形ABDF = 1/2(AB + DF)·EG = 1/2×(4 + 6)×2√2 = 10√2.
(1)证明:
∵点D,E分别为BC,AC边上的中点,
∴DE是△ABC的中位线,
∴DE//AB,AB = 2DE.
∵EF//AB,AF//BE,
∴四边形ABEF是平行四边形.
∵BE = 2DE,
∴AB = BE,
∴四边形ABEF为菱形.
(2)解:如图
 过E作EG⊥AB于G,由
过E作EG⊥AB于G,由(1)可知,DE//AB,AB = 2DE,四边形ABEF为菱形,又
∵AB = 4,
∴DE = 2,BE = EF = AB = 4,
∴DF = DE + EF = 6. 在Rt△EBG中,∠ABE = 45°,
∴△EBG是等腰直角三角形,
∴EG = √2/2BE = 2√2,
∴S四边形ABDF = 1/2(AB + DF)·EG = 1/2×(4 + 6)×2√2 = 10√2.
八(本题满分14分)
23.【模型建立】
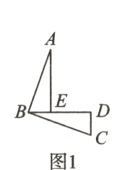
(1)如图1,已知△ABE和△BCD,AB⊥BC,AB = BC,CD⊥BD,AE⊥BD. 用等式写出线段AE,DE,CD的数量关系,并说明理由.(4分)
【模型应用】
(2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上,AE⊥EF,AE = EF. 用等式写出线段BE,AD,DF的数量关系,并说明理由.(5分)
【模型迁移】
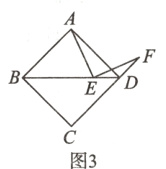
(3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上,AE⊥EF,AE = EF. 请直接用等式写出线段BE,AD,DF的数量关系.(5分)

23.【模型建立】
(1)如图1,已知△ABE和△BCD,AB⊥BC,AB = BC,CD⊥BD,AE⊥BD. 用等式写出线段AE,DE,CD的数量关系,并说明理由.(4分)
【模型应用】
(2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上,AE⊥EF,AE = EF. 用等式写出线段BE,AD,DF的数量关系,并说明理由.(5分)
【模型迁移】
(3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上,AE⊥EF,AE = EF. 请直接用等式写出线段BE,AD,DF的数量关系.(5分)



答案:
(1)解:DE + CD = AE,理由如下:
∵CD⊥BD,AE⊥BD,AB⊥BC,
∴∠ABC = ∠D = ∠AEB = 90°,
∴∠ABE + ∠CBD = ∠C + ∠CBD = 90°,
∴∠ABE = ∠C.
∵AB = BC,
∴△ABE≌△BCD(AAS),
∴BE = CD,AE = BD,
∴DE = BD - BE = AE - CD,
∴DE + CD = AE.
(2)AD = √2BE + DF,理由如下:过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,如图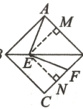
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ADB = ∠CDB = 45°,BD平分∠ADC,∠ADC = 90°,
∴√2AD = √2CD = BD,
∴DE = BD - BE = √2AD - BE.
∵EN⊥CD,EM⊥AD,
∴EM = EN.
∵AE = EF,
∴Rt△AEM≌Rt△FEN(HL),
∴AM = NF.
∵EM = EN,EN⊥CD,EM⊥AD,∠ADC = 90°,
∴四边形EMDN是正方形,
∴ED是正方形EMDN对角线,MD = ND,
∴MD = ND = √2/2DE,NF = ND - DF = MD - DF,
∴NF = AM = AD - MD = AD - √2/2DE,NF = √2/2DE - DF,
∴AD - √2/2DE = √2/2DE - DF,
∴AD = √2DE - DF.
∵DE = √2AD - BE,
∴AD = √2(√2AD - BE) - DF,
∴AD = √2BE + DF.
(3)AD = √2BE - DF.
(1)解:DE + CD = AE,理由如下:
∵CD⊥BD,AE⊥BD,AB⊥BC,
∴∠ABC = ∠D = ∠AEB = 90°,
∴∠ABE + ∠CBD = ∠C + ∠CBD = 90°,
∴∠ABE = ∠C.
∵AB = BC,
∴△ABE≌△BCD(AAS),
∴BE = CD,AE = BD,
∴DE = BD - BE = AE - CD,
∴DE + CD = AE.
(2)AD = √2BE + DF,理由如下:过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,如图

∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ADB = ∠CDB = 45°,BD平分∠ADC,∠ADC = 90°,
∴√2AD = √2CD = BD,
∴DE = BD - BE = √2AD - BE.
∵EN⊥CD,EM⊥AD,
∴EM = EN.
∵AE = EF,
∴Rt△AEM≌Rt△FEN(HL),
∴AM = NF.
∵EM = EN,EN⊥CD,EM⊥AD,∠ADC = 90°,
∴四边形EMDN是正方形,
∴ED是正方形EMDN对角线,MD = ND,
∴MD = ND = √2/2DE,NF = ND - DF = MD - DF,
∴NF = AM = AD - MD = AD - √2/2DE,NF = √2/2DE - DF,
∴AD - √2/2DE = √2/2DE - DF,
∴AD = √2DE - DF.
∵DE = √2AD - BE,
∴AD = √2(√2AD - BE) - DF,
∴AD = √2BE + DF.
(3)AD = √2BE - DF.
查看更多完整答案,请扫码查看


