《2025年课堂点睛八年级数学下册人教版安徽专版》

八(本题满分14分)
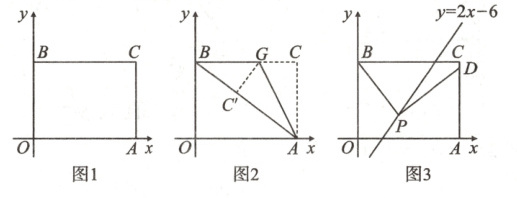
23. 如图1，在矩形$OACB$中，点$A$在$x$轴正半轴上，点$B$在$y$轴正半轴上，点$C$在第一象限，$OA = 8$，$OB = 6$.
(1)直接写出点$C$的坐标：__________；(3分)
(2)如图2，点$G$在$BC$边上，连接$AG$，将$\triangle ACG$沿$AG$折叠，点$C$恰好与线段$AB$上的点$C'$重合，求线段$CG$的长度；(6分)
(3)如图3，$P$是直线$y = 2x - 6$上一点且在$BC$下方，$PD\perp PB$交线段$AC$于点$D$. 若$P$在第一象限，且$PB = PD$，求点$P$的坐标. (5分)

答案：

(1)(8,6)
(2)解：$\because BC = 8$，$AC = 6$，$\therefore AB=\sqrt{BC^{2}+AC^{2}}=\sqrt{64 + 36}=10$，$\because$将$\triangle ACG$沿$AG$折叠，点$C$恰好与线段$AB$上的点$C'$重合，$\therefore AC = AC' = 6$，$CG = C'G$，$\angle C=\angle AC'G = 90^{\circ}$，$\therefore BC' = AB - AC' = 10 - 6 = 4$，在$\triangle BC'G$中，$BG^{2}=C'G^{2}+BC'^{2}$，$\therefore(8 - CG)^{2}=CG^{2}+16$，解得$CG = 3$，$\therefore$线段$CG$的长度为3；
(3)设点$P(a,2a - 6)$，如图3 ，过点$P$作$EF// BC$，交$y$轴于点$E$，交$AC$于点$F$，$\because PD\perp PB$，$\therefore\angle BPD = 90^{\circ}$，$\therefore\angle BPE = 90^{\circ}-\angle DPF$. $\because EF// BC$，$\therefore\angle PFD=\angle ACB = 90^{\circ}$，$\therefore\angle PDF = 90^{\circ}-\angle DPF$，$\therefore\angle BPE=\angle PDF$，$\because\angle BEP=\angle PFD = 90^{\circ}$，$BP = PD$，$\therefore\triangle BPE\cong\triangle PDF(AAS)$. $\therefore PF = BE = OB - OE = 6-(2a - 6)=12 - 2a$，$\because EF = PE + PF = OA = 8$，$\therefore a+(12 - 2a)=8$，解得$a = 4$，$\therefore$点$P$的坐标为$(4,2)$.