《2025年课堂点睛八年级数学下册人教版安徽专版》

22. 秦九韶(1208年～1268年)，字道古，南宋著名数学家. 与李冶、杨辉、朱世杰并称宋元数学四大家. 他精研星象、音律、算术、诗词、弓剑、营造之学. 他于1247年完成的著作《数学九章》中关于三角形的面积公式与古希腊几何学家海伦的成果并称“海伦 - 秦九韶公式”. 它的主要内容是，如果一个三角形的三边长分别是$a$，$b$，$c$，记$p=\frac{a + b + c}{2}$，$S$为三角形的面积，那么$S=\sqrt{p(p - a)(p - b)(p - c)}$。
(1)在$\triangle ABC$中，$BC = 5$，$AC = 6$，$AB = 7$，请用上面的公式计算$\triangle ABC$的面积；(4分)
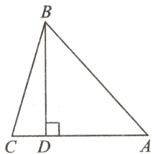
(2)如图，在$\triangle ABC$中，$AB = 9$，$AC = 8$，$BC = 7$，$BD\perp AC$，垂足为$D$，求$CD$的长；(4分)
(3)一个三角形的三边长分别为$a$，$b$，$c$，$S = p = 15$，$a = 10$，求$bc$的值。(4分)

答案：
(1)解：由题意，$p=\frac{BC + AC + AB}{2}=\frac{18}{2}=9$，$\therefore S=\sqrt{p(p - BC)(p - AC)(p - AB)}=\sqrt{9\times4\times3\times2}=6\sqrt{6}$。
(2)由题意，$p=\frac{AB + AC + BC}{2}=\frac{24}{2}=12$，$\therefore S_{\triangle ABC}=\sqrt{p(p - BC)(p - AC)(p - AB)}=\sqrt{12\times5\times4\times3}=12\sqrt{5}$。又$S_{\triangle ABC}=\frac{1}{2}BD\cdot AC$，$AC = 8$，$\therefore BD=\frac{2S_{\triangle ABC}}{AC}=\frac{2\times12\sqrt{5}}{8}=3\sqrt{5}$。$\therefore$在$Rt\triangle BDC$中，$CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{7^{2}-(3\sqrt{5})^{2}}=2$。
(3)由题意，$p=\frac{a + b + c}{2}=\frac{10 + b + c}{2}=15$，$S = p=\sqrt{p(p - a)(p - b)(p - c)}$，$\therefore b + c = 20$，$(15 - b)(15 - c)=3$。$\therefore bc = 78$。