《2025年课堂点睛八年级数学下册人教版安徽专版》

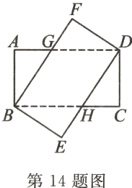
14. 两个全等的矩形纸片ABCD和BEDF按图所示的位置重叠在一起，已知$AB = 2\sqrt{3}$，$AD = 6$.
（1）用准确的语言描述重叠的四边形BHDG的形状：__________；
（2）按照既得结论，四边形BHDG的面积是__________.

答案：
(1)菱形
(2)8√3

15. 计算：
（1）$(\sqrt{12}+\sqrt{20})-(\sqrt{3}-\sqrt{5})$；（4分）
（2）$\frac{\sqrt{12}\times\sqrt{6}}{\sqrt{8}}+(\sqrt{2}-1)^2$.（4分）

答案：
(1)解：原式=2√3+2√5 - √3+√5=√3+3√5；
(2)解：原式=3+2 - 2√2+1=6 - 2√2.

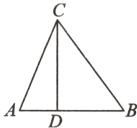
16. 如图，在$\triangle ABC$中，点D在AB上，$AC = 2\sqrt{5}$，$BC = 5$，$BD = 3$，$CD = 4$. 求$\triangle ABC$的面积.

答案： 解：在△BCD中，CD²+BD²=4²+3²=25，BC²=5²=25，
∴BC²=CD²+BD².
∴∠CDB=90°.
∴∠ADC=180° - ∠CDB=90°.
∴AD=√(AC² - CD²)=√((2√5)² - 4²)=2.
∴AB=AD+BD=2+3=5.
∴S△ABC=1/2BA·CD=1/2×5×4=10.

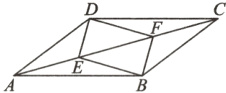
17. 已知：如图，在平行四边形ABCD中，点E、F在对角线AC上，且$AF = CE$. 求证：四边形BFDE是平行四边形.

答案：
证明：如图: 连接BD，交AC于点O.
∵四边形ABCD是平行四边形，O是对角线AC、BD的交点.
∴AO=CO.又
∵点E、F在对角线AC上，且AF=CE，
∴AF - AO=CE - CO，即FO=EO，
∵四边形ABCD是平行四边形，
∴BO=DO，
∵FO=EO，
∴四边形BFDE是平行四边形.