《2025年课堂点睛八年级数学下册人教版安徽专版》

20. 现政府想将某石榴基地规模扩大，计划种植红籽石榴和白籽石榴共60亩，有关数据如下表：

(1)设种植红籽石榴$x$亩，两种石榴的总收益为$y$万元，求$y$关于$x$的函数解析式(收益 = 销售额 - 成本)；(5分)
(2)若计划投入的成本不超过260万元，要使获得的收益最大，基地应种植红籽石榴和白籽石榴分别多少亩？(5分)

答案：
(1)解：由题意可得$y=(6 - 4.8)x+(5 - 4)(60 - x)=0.2x + 60$，即$y$关于$x$的函数解析式是$y = 0.2x + 60$.
(2)由题意可得$4.8x + 4(60 - x)\leq260$，解得$x\leq25$. $\because y = 0.2x + 60$，$\therefore$当$x = 25$时，$y$取最大值，此时$y = 65$，$60 - x = 35$. 答：要使获得的收益最大，基地应种红籽石榴25亩，白籽石榴35亩.

六(本题满分12分)
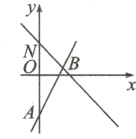
21. 如图，在平面直角坐标系中，直线$y = 2x + m$与$y$轴交于点$A$，与$y = - x + 5$交于点$B(4,n)$，$C$为直线$y = - x + 5$上任意一点.
(1)求$m$，$n$的值；(6分)
(2)求使线段$AC$最短时点$C$的坐标和$AC$的最小值. (6分)

答案：

(1)解：$\because$点$B(4,n)$在直线$y = -x + 5$上，$\therefore n = -4 + 5 = 1$，$\therefore B(4,1)$. $\because$点$B(4,1)$在直线$y = 2x + m$上，$\therefore 8 + m = 1$，解得$m = -7$.
(2)如图 ，过点$A$作直线$y = -x + 5$的垂线，垂足为$C$，此时线段$AC$最短. 作$CM\perp AN$于$M$. $\because$直线$y = -x + 5$与$y$轴交于点$N(0,5)$，与$x$轴交于点$(5,0)$，直线$y = 2x - 7$与$y$轴交于点$A(0,-7)$，$\therefore AN = 12$，$\angle ANC = 45^{\circ}$，$\because\angle ACN = 90^{\circ}$，$\therefore AC = CN$，$\because CM\perp AN$，$\therefore AM = CM=\frac{1}{2}AN = 6$，$\therefore AC = 6\sqrt{2}$，$OM = 1$，$\therefore C(6,-1)$.

七(本题满分12分)
22. 某体育用品商店准备用不超过2800元购进足球和篮球共计60个，已知一个篮球的进价为50元，售价为65元；一个足球的进价为40元，售价为50元.
(1)若购进$x$个篮球，购进这批球共花费$y$元，求$y$与$x$之间的函数关系式；(不要求写出$x$的取值范围)(4分)
(2)设售出这批球共盈利$w$元，求$w$与$x$之间的函数关系式；(不要求写出$x$的取值范围)(4分)
(3)体育用品商店购进篮球和足球各多少个时，售出后获得的利润最大？最大利润是多少？(4分)

答案：
(1)解：若购进$x$个篮球，则购进了$(60 - x)$个足球. 可得$y = 50x + 40(60 - x)=10x + 2400$，$\therefore y$与$x$之间的函数关系式为$y = 10x + 2400$.
(2)$w=(65 - 50)x+(50 - 40)(60 - x)=15x + 10(60 - x)=5x + 600$，$\therefore w$与$x$之间的函数关系式为$w = 5x + 600$.
(3)由题意可得$10x + 2400\leq2800$，解得$x\leq40$. $\therefore 0\leq x\leq40$且$x$为整数. 在$w = 5x + 600$中，$\because 5＞0$，$\therefore w$随$x$的增大而增大. $\therefore$当$x = 40$时，$w$取得最大值，此时$w = 800$，$60 - x = 20$. 答：当购进40个篮球，20个足球时，售出后获得的利润最大，最大利润是800元.